Жак Арсак - Программирование игр и головоломок

См. головоломку 29. — Примеч. пер.

В математике для решения этой задачи есть полезная формула Ньютона-Лейбница:

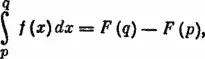
где F —функция, определяемая условием F ( x ) = f ( x ), x ∊ [ p , q ]. Впрочем, все эти интегралы нам не понадобятся, так как у этой формулы есть гораздо более простой аналог для сумм: a i + a i +1+ … + a j = b j − b i −1, где последовательность { b } определяется условием, что b k − b k −1= а k для любого k от 1 до n . Последовательность { b } легко построить: b 0= 0, b k +1= b k + a k +1. Для последовательности { b } задача ставится так: найти такие i < j , что разность b j − b i максимальна. С этой задачей уже легче справиться. — Примеч. ред.

Вот пара условий, которая не обладает этим свойством: t : x ≠ 0; u : sin(1/ x ) > 0. — Примеч. ред.

Прочтя весь этот ужас, я решил провести решение, основанное на методике из курса программирования механико-математического факультета МГУ.

Каждой последовательности чисел { a 1, а 2, …, a i} ( i ≥ 1) сопоставим число lmax, равное максимальной длине равнинного участка этой последовательности. Очевидно, что lmax ({ a 1}) = 1. Пусть мы знаем lmax ({ a 1, а 2, …, a i }). Как вычислить величину lmax ({ a 1, …, a i , a i +1})? Добавление элемента a i +1к последовательности { a 1, а 2, …, a i} не затрагивает равнинных участков этой последовательности, кроме, быть может, последнего. Если a i +1= a i, то длина этого последнего участка — назовем ее llast ({ a 1, …, a i}) — увеличивается на единицу. Если величина llast ({ a 1, …, a i, a i +1}) окажется при этом больше величины lmax ({ a 1, а 2, …, a i}), то это значит, что последний равнинный участок в последовательности { a 1, а 2, …, a i, a i +1} по крайней мере на 1 длиннее всех предыдущих, и, значит, lmax ({ a 1, а 2, …, a i, a i +1}) = llast ({ a 1, а 2, …, a i, a i +1}).

Введем четыре величины:

i — число рассмотренных членов последовательности,

lmax — максимальная длина равнинного участка для рассмотренных элементов,

llast — длина последнего равнинного участка для рассмотренных элементов,

xlast — последний рассмотренный элемент последовательности (он равен а[i]).

Теперь приведем без пояснений программу, которая вычисляет lmax ({ a 1, …, a n}) по индукции.

i := 1; lmax := 1; llast := 1; xlast := a [1]

нц пока i < n

x := a [ i + 1]

если x = xlast тоllast := llast + 1

иначеllast := 1 кесли

еслиllast > lmax тоlmax := llast кесли

xlast := x

i := i + 1

кц

вывод lmax

Подробнее об этой индуктивной методике можно прочитать в книге: А. Г. Кушниренко, Г. В. Лебедев. Программирование для математиков. — М.: Наука, 1988. — Примеч. ред.