Жак Арсак - Программирование игр и головоломок
- Название:Программирование игр и головоломок
- Автор:
- Жанр:
- Издательство:Наука. Гл. ред. физ.-мат. лит.
- Год:1990
- Город:Москва
- ISBN:5-02-013959-9
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Жак Арсак - Программирование игр и головоломок краткое содержание
Рассматриваются способы программирования различных занимательных игр и головоломок с числами, геометрическими фигурами и др. Изложение большинства игр и головоломок ведется в несколько этапов. Сначала разъясняется сама постановка задачи и требования, предъявляемые к алгоритму ее решения.
В следующем разделе книги обсуждается сам алгоритм и возможные пути его реализации.
В конце книга по многим играм и головоломкам даются наброски их программной реализации. Используемый при этом язык типа Паскаля допускает перевод на другие широко распространенные языки программирования.
Для начинающих программистов, студентов вузов и техникумов.
Программирование игр и головоломок - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Удобно пользоваться первыми разностями для функции f 4:
d ( р ) = f 4( p + 1) − f 4( p ).
Два приведенных выше соотношения могут быть переписаны следующим образом:
d ( p − 1) < 2 n - p -1, d ( р ) ≥ 2 n - p- 2.
Интересно рассматривать даже не d ( р ), а скорее 2 pd ( р ) = g ( р ):
g ( р − 1) ~ 2 n -2≤ g ( р ).
Можно еще упростить запись, беря не g ( р ), а величину
h ( р ) = log 2( g ( р )) = р + Iog 2( d ( р )).
Тогда получаем
h ( р − 1) < n − 1 ≤ h ( р ).
При данном n величина р — наименьшее целое, для которого h больше или равно n − 2.
Приведем здесь первые из полученных таким образом значений:
| n | q | f 4 | p | d | h |
| 0 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 2 | 2 | |
| 2 | 3 | 2 | 3 | ||
| 3 | 2 | 5 | 1 | 4 | 5 |
| 4 | 9 | 1 | 4 | 6 | |
| 5 | 13 | 1 | 4 | 7 | |
| 6 | 3 | 17 | 3 | 8 | 9 |
| 7 | 25 | 3 | 8 | 10 | |
| 8 | 33 | 4 | 8 | 11 | |
| 9 | 41 | 5 | 8 | 12 | |
| 10 | 4 | 49 | 6 | 16 | 14 |
| 11 | 65 | 6 | 16 | 15 |
Мы добавили в таблицу переменное q , связанное с «треугольными» числами. Для n = q ( q + 1)/2 действительно убеждаемся, что
h ( р ) = h ( р − 1) + 2
в то время как для других n
h ( p ) = h ( p − 1) + 1.
Исходя из n , можно вычислить q :
q = целая_часть (( 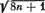 − 1)/2).
− 1)/2).
Имеем
h ( n ) = n + целая_часть (( 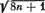 − 1)/2).
− 1)/2).
Покажите это по индукции. Исходя отсюда, вычисляется все. Таким образом, если n дано, то р — наименьшее целое, большее или равное
(2 n − 1 − 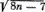 )/2.
)/2.
Игра 35.
Возьмем, например, игру с 50 дисками. Она реализуется переносом сначала 40 дисков на запасной стержень, а затем 10 последних дисков со стержня 0 на стержень 1, с использованием при этом только трех свободных стержней. Наконец, остается перенести начальные 40 самых маленьких дисков с запасного стержня на первый стержень, используя все 4 стержня.
Чтобы переместить 40 дисков с 4 стержнями, сводим задачу к перемещению 31 диска с 4 стержнями, а затем 9 с 3 стержнями…
Таким образом, дело сводится к разбиению 50 дисков на 8 сегментов:

Каждый сегмент перемещается с использованием 3 стержней, в чем мы следуем итеративной стратегии, которая уже описана выше. Единственный вопрос — это правильный выбор запасных стержней.
Договоримся работать с тремя стержнями 0, 1, 2, так что стержень 3 остается пустым и служит запасным стержнем при любом перемещении какого-либо сегмента. Более точно, перемещение сегмента р со стержня d на стержень а осуществляется с помощью изученной выше процедуры Н , в которой запасным стержнем является стержень 3.
Сегмент 1 перемещается в каждый из двух ходов подряд (под ходом я понимаю последовательность операций, реализующих процедуру Н ), всегда в одном и том же направлении.
Мы сохраняем предыдущую итеративную стратегию, но понимаем ее как стратегию для сегментов. На компьютере это может пройти очень быстро. Вполне вероятно, что робот может осуществить одно перемещение за несколько секунд. Тогда на всю игру потребуется не более чем несколько часов…
Игра 36.
Соотношение SG ( p , q ) = 0 означает, что вы не можете достичь ситуации с числом Спрага-Грюнди, равным нулю, удаляя не более 2 q спичек из кучки с р спичками. Если вы исходите из SG ( р , q ' < q ), то вы не можете удалить столько же спичек и, следовательно, нет опасности, что вы получите число SG , равное нулю.
Предположим, что SG ( p i , 1) = 0.
Исходя из p i + 1, я могу удалить 1 спичку и получить пару p i , 1. Следовательно, SG ( p i + 1, q ) ≠ 0.
Исходя из p i + 2, я для любого q всегда могу удалить две спички, но тогда я получаю SG ( p i , 2) ≠ 0, и, следовательно,
SG ( p i + 2, 1) = 0.
Если в p i имеем q i > 1, то тогда мы этого не получим и SG ( p i + 2, 1) ≠ 0. Но в p i + 3, удаляя единственную спичку, получаем пару p i + 2, 1 c SG ≠ 0, или же, удаляя две спички, получаем пару p i + 1, 2 с ненулевым числом SG . Следовательно, SG ( p i + 3, 1) = 0.
Все оставшееся уже очень хорошо подготовлено. Рассмотрите точку р , для которой диагональ пересекает ось р = 0, не пересекая положений с нулевым SG . Эта прямая задается уравнением x + у = р . Она пересекает ось x = 0 в точке у = р . Нельзя взять в точности р спичек, — можно не больше р − 1. Следовательно, в этой точке
q = целая_часть (( р − 1)/2).
Рассмотрим теперь точку, абсцисса которой есть число Фибоначчи: р = fib ( s ).
Нужно показать, что прямая x + у = fib ( s ) не пересекает точек с ненулевыми SG , кроме x = 0. Рассмотрим сначала точку
х = fib ( s − 1).
В этой точке
у = fib ( s ) − fib ( s − 1) = fib ( s − 2).
При p = fib ( s − 1)
q = целая_часть ((fib ( s − 1) − 1)/2).
Нужно показать, что для каждого s
целая_часть ((fib ( s − 1) − 1)/2) < fib ( s − 2),
или, что равносильно,
fib ( s − 1) < 2 * fib ( s − 2) + 1.
Но
fib ( s − 1) = fib ( s − 2) + fib ( s − 3)
и
fib ( s − 3) < fib ( s − 2).
Следовательно, рассматриваемая диагональ не пересекает точек с нулевым SG в fib ( s − 1). Она не может пересекать их и между s − 1 и s , поскольку эта часть воспроизводит то, что происходит в интервале от 1 до fib ( s − 2), а диагональ, выходящая из fib ( s − 2), не пересекает точек с нулевым SG до оси q .
Вы без труда завершите это доказательство.
6. Комбинаторные задачи
Головоломка 28.
Действительно ли вам что-то еще нужно сообщать? Тогда я немного уточню способ поддержания части от 1 до р в порядке неубывания. Исходим ив упорядоченного по неубыванию вектора a 1, a 2, …, а р . Вы последовательно заменяете элемент а р элементами а i , где i направлен по убыванию. Вы последовательно получите
a 1, a 2, …, а р -1, а р ,
a 1, a 2, …, а р , а р -1,
a 1, a 2, …, а р -3, а р -1, а р , а р -2.
По индукции, предположим, что в некоторый момент вы получили
Читать дальшеИнтервал:
Закладка:









