Джулиан Бакнелл - Фундаментальные алгоритмы и структуры данных в Delphi

function TtdInputBitStream.ReadBit : boolean;

begin

{если в текущей аккумуляторной переменной никаких битов не осталось, необходимо выполнить считывание следующего байта аккумуляторной переменной и сбросить значение маски}

if (FMask = 0) then begin

if (FBufPos >= FBufEnd) then

ibsReadBuffer;

FAccum := byte(FBuffer [FBufPos] );

inc(FBufPos);

FMask := 1;

end;

{извлечь следующий бит}

Result := (FAccum and FMask) <> 0;

FMask := FMask shl 1;

end;

После того, как мы выяснили, как выполняется считывание отдельного бита, покажем, что запись отдельного бита - тот же самый процесс, только выполняемый в обратном порядке. Код метода WriteBit, в котором единственный бит передается как булево значение - true, если бит установлен, и false, если он очищен - приведен в листинге 11.4.

Листинг 11.4. Запись отдельного бита в объект TtdOutputBitStream

procedure TtdOutputBitStream.WriteBit(aBit : boolean);

begin

{установить следующий свободный бит}

if aBit then

FAccum := (FAccum or FMask);

FMask := FMask shl 1;

{/при отсутствии свободных битов в текущей аккумуляторной переменной ее значение нужно записать в буфер и сбросить значение аккумуляторной переменной и маски}

if (FMask = 0) then begin

byte(FBuffer[FBufPos]) := FAccum;

inc(FBufPos);

if (FBufPos >= StreamBufferSize) then

obsWriteBuffer;

FAccum := 0;

FMask := 1;

end;

end;

Поскольку обработка всегда начинается при значении аккумуляторного байта (FAccum) равном нулю, нужно всего лишь записать эти биты установки, а не очистить их. Мы снова используем маску (EMask), содержащую единственный бит установки, но на этот раз чтобы установить соответствующий бит, после чего выполняем операцию OR (ИЛИ) между маской и значением аккумуляторной переменной. Затем мы сдвигаем маску влево на один бит, подготавливая к обработке следующий бит. Однако если теперь значение маски равно нулю, потребуется сохранить аккумуляторный байт в буфере (записывая буфер в базовый поток, если буфер полон), а затем сбросить значение аккумуляторного байта и маски.

Полный код обоих классов TtdInputBitStrem и TtdOutputBitStrem можно найти на Web-сайте издательства, в разделе материалов. После выгрузки материалов отыщите среди них файл TDStrms.pas. Полный код содержит также подпрограммы одновременного считывания и записи нескольких битов - либо восьми битов отдельного байта (ReadByte и WriteByte), либо переменного числа байтов из массива байтов (ReadBits и WriteBits). Для доступа к отдельным битам все эти дополнительные подпрограммы используют одну и ту же методологию манипуляции битами. Просто соответствующие операции выполняются в цикле.

Теперь, когда в нашем распоряжении имеется класс потока битов, им можно воспользоваться при рассмотрении алгоритмов сжатия и восстановления данных. Мы начнем с исследования алгоритмов кодирования с минимальной избыточностью, а затем рассмотрим более сложное сжатие с применением словаря.

Мы приведем подробное описание трех алгоритмов кодирования с минимальной избыточностью: кодирование Шеннона-Фано (Shannon-Fano), кодирование Хаффмана (Huffman) и сжатие с применением скошенного дерева (splay tree compression), однако рассмотрим реализации только последних двух алгоритмов (алгоритм кодирования Хаффмана ни в чем не уступает, а кое в чем даже превосходит алгоритм кодирования Шеннона-Фано). При использовании каждого из этих алгоритмов входные данные анализируются как поток байтов, и различным значениям байтов тем или иным способом присваиваются различные последовательности битов.

Первый алгоритм сжатия, который мы рассмотрим - кодирование Шеннона-Фано, названное так по имени двух исследователей, которые одновременно и независимо друг от друга разработали этот алгоритм: Клода Шеннона (Claude Shannon) и Р. М. Фано (R. М. Fano). Алгоритм анализирует входные данные и на их основе строит бинарное дерево минимального кодирования. Используя это дерево, затем можно выполнить повторное считывание входных данных и закодировать их.

Чтобы проиллюстрировать работу алгоритма, выполним сжатие предложения "How much wood could a woodchuck chuck?" ("Сколько дров мог бы заготовить дровосек?") Прежде всего, предложение необходимо проанализировать. Просмотрим данные и вычислим, сколько раз в предложении встречается каждый символ. Занесем результаты в таблицу (см. таблицу 11.1).

Таблица 11.1. Частота появления символов в примере предложения

Символ - Количество появлений

Пробел - 6

c - 6

o - 6

u - 4

d - 3

h - 3

w - 3

k - 2

H - 1

a - 1

l - 1

m - 1

? - 1

Теперь разделим таблицу на две части, чтобы общее число появлений символов в верхней половине таблицы приблизительно равнялось общему числу появлений в нижней половине. Предложение содержит 38 символов, следовательно, верхняя половина таблицы должна отражать приблизительно 19 появлений символов. Это просто: достаточно поместить разделительную линию между строкой о и строкой и. В результате этого верхняя половина таблицы будет отражать появление 18 символов, а нижняя - 20. Таким образом, мы получаем таблицу 11.2.

Таблица 11.2. Начало построения дерева Шеннона-Фано

Символ - Количество появлений

Пробел - 6

c - 6

o - 6

------------------------------------ разделительная линия 1

u - 4

d - 3

h - 3

w - 3

k - 2

H - 1

a - 1

l - 1

m - 1

? - 1

Теперь проделаем то же с каждой из частей таблицы: вставим линию между строками так, чтобы разделить каждую из частей. Продолжим этот процесс, пока все буквы не окажутся разделенными одна от другой. Результирующее дерево Шеннона-Фано представлено в таблице 11.3.

Таблица 11.3. Завершенное дерево Шеннона-Фано Символ Количество появлений

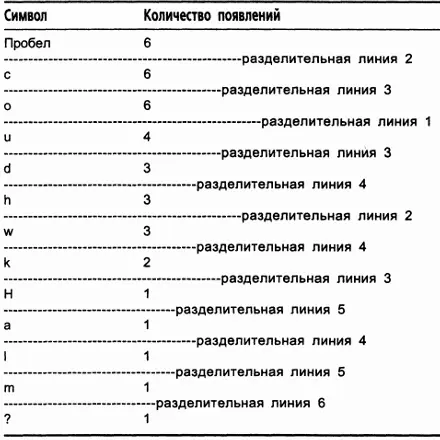
Я намеренно изобразил разделительные линии различными по длине, чтобы разделительная линия 1 была самой длинной, разделительная линия 2 немного короче и так далее, вплоть до самой короткой разделительной линии 6. Этот подход обусловлен тем, что разделительные линии образуют повернутое на 90° бинарное дерево (чтобы убедиться в этом, поверните таблицу на 90° против часовой стрелки). Разделительная линия 1 является корневым узлом дерева, разделительные линии 2 - двумя его дочерними узлами и т.д. Символы образуют листья дерева. Результирующее дерево в обычной ориентации показано на рис. 11.1

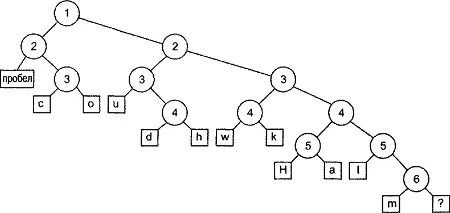
Рисунок 11.1. Дерево Шеннона-Фано

Все это очень хорошо, но как оно помогает решить задачу кодирования каждого символа и выполнения сжатия? Что ж, чтобы добраться до символа пробела, мы начинаем с коневого узла, перемещаемся влево, а затем снова влево. Чтобы добраться до символа с, мы смещаемся влево из корневого узла, затем вправо, а затем влево. Для перемещения к символу о потребуется сместиться влево, а затем два раза вправо. Если принять, что перемещение влево эквивалентно нулевому биту, а вправо - единичному, можно создать таблицу кодирования, приведенную в таблице 11.4.