Михаил Адаменко - Основы классической криптологии. Секреты шифров и кодов

Как известно, чем меньше столбцов и строк в квадратной таблице, тем меньше вариантов построения на ее основе магического квадрата Так, например, для таблицы, состоящей из трех столбцов и трех строк, известен всего лишь один вариант заполнения ячеек цифрами от 1 до 9, в результате которого получится магический квадрат. Такая таблица будет выглядеть так:

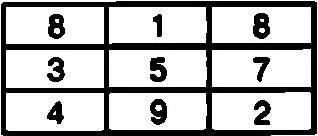
Нетрудно подсчитать, что сумма цифр в каждом столбце, в каждой строке и в каждой большой диагонали составляет одно и то же число и равна 15.

При использовании шифров, основанных на магических квадратах, один из простейших алгоритмов шифрования заключается в том, что в ячейки таблицы вместо цифр магического квадрата вписываются по порядку буквы открытого текста. Так, например, вместо цифры 1 в соответствующую ей ячейку следует записать первую букву сообщения, вместо цифры 2 — вторую букву, вместо цифры 3 — третью букву и так далее.

В качестве примера зашифруем с помощью этого магического квадрата открытый текст РАЗВЕДЧИК При этом в ячейку с цифрой 1 следует записать букву Р, в ячейку с цифрой 2 — букву А, в ячейку с цифрой 3 — букву 3 и так до конца сообщения. В результате таблица примет следующий вид:

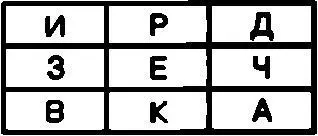
Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек первой строки, затем из ячеек второй строки и так далее.

В окончательном виде криптограмма для открытого текста РАЗВЕДЧИК будет выглядеть так:

ИРД ЗЕЧ ВКА

Получив такую шифрограмму, получатель для расшифровки сообщения должен сначала заполнить таблицу буквами криптограммы, а затем из соответствующих ячеек выписать буквы открытого текста в порядке, определяемом цифрами используемого магического квадрата.

Необходимо отметить, что утверждение о существовании лишь одного магического квадрата размером 3x3 для цифр от 1 до 9 не касается случаев, когда другие магические квадраты могут быть образованы из первоначального с помощью поворота таблицы или отражения строк и столбцов.

Один из таких производных квадратов может выглядеть следующим образом:

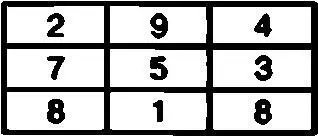
Такой магический квадрат также с успехом можно использовать для шифрования коротких сообщений в соответствии с приведенным выше алгоритмом.

В одном из древних индийских храмов исследователи обнаружили квадратную таблицу, которая при более подробном изучении оказалась одним из самых первых известных магических квадратов. По мнению некоторых историков, эта таблица была создана в XII веке.

Ячейки данной таблицы, состоящей из четырех столбцов и четырех строк, заполнены числами от 1 до 16 так, что сумма всех чисел, расположенных в одном столбце, в одной строке и на одной диагонали, составляет одно и то же число, а именно 34. Более того, сумма чисел в четырех ячейках, образующих квадратные таблицы внутри данного магического квадрата, также составляет 34.

Порядок заполнения ячеек в этой таблице выглядит следующим образом:

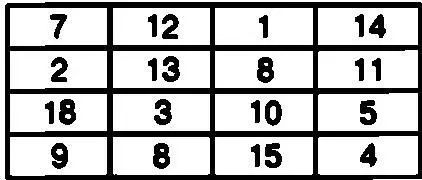
Естественно, что такой магический квадрат также можно использовать для шифровки короткого сообщения, содержащего до шестнадцати знаков.

В качестве примера зашифруем, например, открытый текст СЕКРЕТНАЯ ВСТРЕЧА. Для шифрования данного сообщения с использованием рассмотренного ранее алгоритма необходимо сначала вставить в ячейки таблицы вместо цифр буквы открытого текста. При этом вместо цифры 1 в соответствующую ячейку следует вставить первую букву открытого текста, в рассматриваемом примере это будет буква С. Вместо цифры 2 в соответствующую ячейку следует вставить вторую букву открытого текста, то есть букву Е, и так далее.

В результате такой замены шифровальная таблица примет следующий вид:

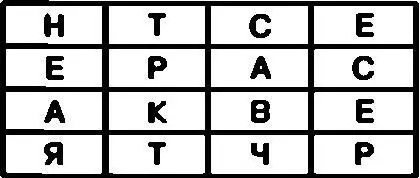
Теперь для создания криптограммы достаточно последовательно выписать буквы из ячеек первой строки, затем из ячеек второй строки и так далее.

В окончательном виде криптограмма для открытого текста СЕКРЕТНАЯ ВСТРЕЧА будет выглядеть так:

НТСЕ ЕРАС АКВЕ ЯТЧР

Для того чтобы расшифровать эту шифрограмму, получатель сообщения должен сначала заполнить таблицу известных ему размеров буквами криптограммы, а затем из соответствующих ячеек выписать буквы открытого текста в порядке, определяемом цифрами используемого магического квадрата.

По утверждению некоторых источников, классических магических квадратов размером 4x4 существует всего 12. При этом другие магические квадраты тех же размеров могут быть образованы из первоначального, например с помощью поворота таблицы или отражения строк и столбцов. Общее число таких производных магических квадратов разными специалистами оценивается от нескольких сотен до нескольких тысяч. С учетом того, что любой из упомянутых магических квадратов может быть использован для шифрования сообщения, задача взлома шифра для незаконного пользователя с помощью подбора необходимой таблицы вручную становится практически невыполнимой.

Известный математик, астролог и криптограф Леонард Эйлер, долгое время работавший в России в XVIII веке, является автором известной таблицы, состоящей из восьми столбцов и восьми строк.

Все клетки так называемого квадрата Эйлера заполнены числами от 1 до 64 так, что сумма всех чисел, расположенных в одном столбце и в одной строке, составляет одно и то же число, а именно 260. Более того, если данную таблицу разделить на четыре квадратные таблицы, то и в каждой из них сумма чисел в ячейках одного столбца и одной строки также будет одинакова и составит 130. Таким же свойством обладает и квадрат размером 4x4, составленный из ячеек, расположенных в центральной части большой таблицы.

Порядок заполнения ячеек в квадрате Эйлера выглядит следующим образом:

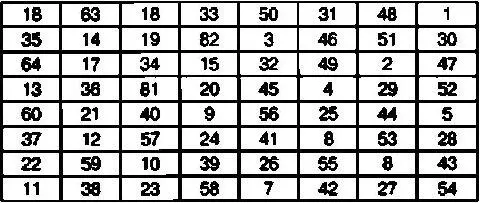
Нетрудно заметить, что с математической точки зрения данная таблица не является классическим магическим квадратом, поскольку суммы чисел в ячейках, образующих диагонали, не равны между собой. В то же время квадрат Эйлера можно использовать для шифрования сравнительно длинных сообщений, используя алгоритм шифрования, рассмотренный ранее для классических магических квадратов.