Евгений Ширшов - Финансово-экономические расчеты в Excel

В Excel существует группа функций, предназначенная для расчета финансовых операций по кредитам, ссудам, займам. Эти расчеты основаны на концепции временной стоимости денег, относящихся к разным моментам времени. Эта группа функций охватывает следующие расчеты:

– определение наращенной суммы (будущей стоимости);

– определение начального значения (текущей стоимости);

– определение срока платежа и процентной ставки;

– расчет периодических платежей, связанных с погашением займов.

Понятие будущей стоимости основано на принципе неравноценности денег, относящихся к разным моментам времени. Вложения, сделанные сегодня, в будущем составят большую величину. Эта группа функций позволяет рассчитать:

– будущую или наращенную стоимость серии фиксированных периодических платежей, а также будущую стоимость текущего значения вклада или займа при постоянной процентной ставке;

– будущее значение инвестиции после начисления сложных процентов при переменной процентной ставке.

Во многих задачах используется и понятие текущей (современной) стоимости будущих доходов и расходов. Это понятие базируется на положении о том, что на начальный момент времени полученная в будущем сумма денег имеет меньшую стоимость, чем ее эквивалент, полученный в начальный момент времени.

Согласно концепции временной стоимости денег, расходы и до ходы, не относящиеся к одному моменту времени, можно сопоставить путем приведения к одному сроку (т.е. путем дисконтирования). Текущая стоимость получается как результат приведения будущих доходов и расходов к начальному периоду времени. Excel содержит ряд функций, которые позволяют рассчитать:

– текущую стоимость единой суммы вклада (займа) и фиксированных периодических платежей;

– чистую текущую стоимость будущих периодических расходов и поступлений переменной величины;

– чистую текущую стоимость нерегулярных расходов и поступлений переменной величины.

Функции для определения срока платежа и процентной ставки позволяют находить величины, расчет которых весьма затруднен, если ведется вручную. К ним относятся:

– общее число периодов постоянных выплат, необходимых для достижения заданного будущего значения; число периодов, через которое начальная сумма займа (вклада) достигнет заданного значения;

– значение постоянной процентной ставки за один период серии фиксированных периодических платежей; значение ставки процента по вкладу или займу.

При выпуске ценных бумаг, заключении финансовых контрактов, займах на долговом соглашении указывается годовая номинальная процентная ставка и период начисления (год, полугодие, квартал).

Начисление процентов по номинальной ставке производится по формуле сложных процентов. Годовая ставка, обеспечивающая тот же доход, что и номинальная ставка после начисления сложных процентов, – это эффективная процентная ставка. Номинальная и эффективная процентная ставки эквивалентны по финансовому результату.

Функции Excel также позволяют вычислять следующие величины, связанные с периодическими выплатами:

– периодические платежи, осуществляемые на основе постоянной процентной ставки и не меняющиеся за все время расчета;

– платежи по процентам за конкретный период;

– сумму платежей по процентам за несколько периодов, идущих основные платежи по займу (за вычетом процентов) за конкретный период;

– сумму основных платежей за несколько периодов, идущих подряд.

Все эти величины вычисляются, например, при расчете схемы равномерного погашения займа. Допустим, что заем погашается одинаковыми платежами в конце каждого расчетного периода. Будущая стоимость этих платежей будет равна сумме займа с начисленными процентами к концу последнего расчетного периода, если в нем предполагается полное погашение займа.

С другой стороны, текущая стоимость выплат по займу должна равняться настоящей сумме займа. Если известна сумма займа, ставка процента, срок, на который выдан заем, то можно рассчитать сумму постоянных периодических платежей, необходимых для равномерного погашения займа.

Задача : Предположим, что открыт льготный (не облагаемый налогами) пенсионный счет. При этом планируется вносить на счет 2000$ в начале каждого года в расчете на среднюю скорость оборота 11 % в год на протяжении всего срока. Если считать, что клиенту сейчас 30 лет, то какая сумма будет аккумулирована на его счету, когда ему исполниться 65 лет, и если клиент открыл счет три года назад и на настоящий момент уже накопил 7500$?

Ответ : = БС (11 %;35; -2000;; 1) через 35 лет на счете клиента будет 758328,81$; = БС (11 %; 35; -2000; -7500; 2) с накоплением через 35 лет на счете клиента будет 1047640,19$. В этих двух примерах аргумент тип равен 1, поскольку выплаты производятся в начале периодов . Если опустить аргумент тип в последней формуле , т . е . предполагается , что деньги вносятся на счет в конце каждого года , Excel возвращает значение 972490,49$. Разница составляет больше 75000$!

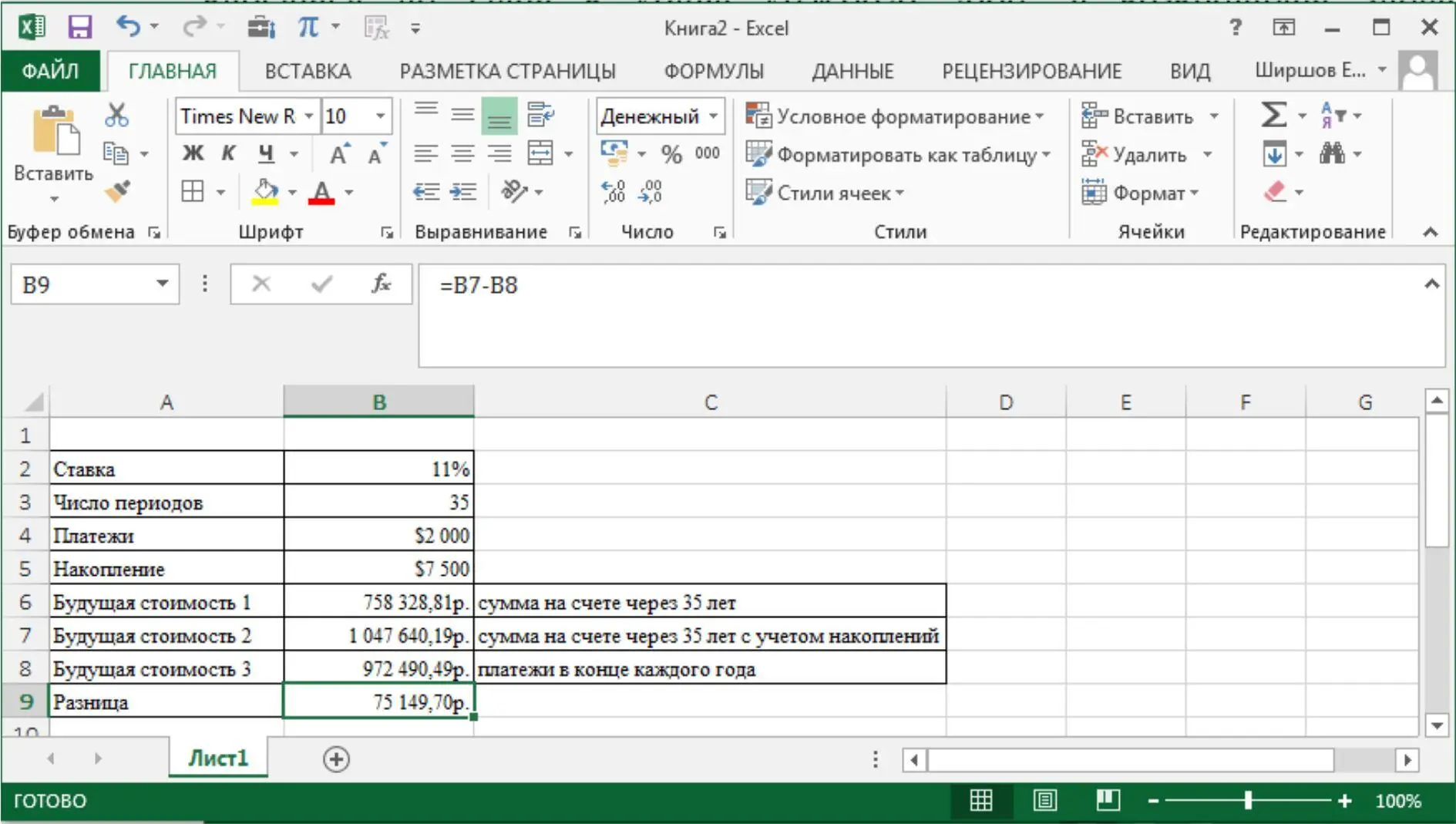
Рис. 5. Пример решения задачи по теме: «Функции для расчета операций по кредитам и займам»

1. Рассчитать, какая сумма окажется на счете, если 27 тыс. руб. положенына 33 года под 13,5 % годовых. Проценты начисляются каждые полгода.

2. Предположим, есть два варианта инвестирования средств в течение 4лет: в начале каждого года под 26 % годовых или в конце каждого года под 38 % годовых. Пусть ежегодно вносится 300 тыс. руб. Определить, сколько денег окажется на счете в конце 4-го года для каждого варианта.

3. Предположим, Вы хотите зарезервировать деньги для специального проекта, который будет осуществлен через год. Предположим, Вы собираетесь вложить 1000 рублей под 6 % годовых (что составит в месяц 6 %/12 или 0,5 %). Вы собираетесь вкладывать по 100 рублей в начале каждого следующего месяца в течение следующих 12 месяцев. Сколько денег будет на счету в конце 12 месяцев?

4. Рассчитать, какая сумма будет на счете, если сумма размером5000 тыс. руб. размещена под 12 % годовых на 3 года, а проценты начисляются каждые полгода.

5. По вкладу размером 2000 тыс. руб. начисляется 10 % годовых.Рассчитать, какая сумма будет на сберегательном счете через 5 лет, если проценты начисляются ежемесячно.