Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

А если мы сложим «соседей» числа из последовательности Люка, получим результат, который будет ровно в 5 раз больше соответствующего ему по позиции числа Фибоначчи:

Если перемножить между собой соответствующие друг другу числа двух последовательностей, мы получим еще одно число последовательности Фибоначчи!

Последнее может быть доказано с помощью алгебры и формул Бине (а именно ( x – y )( x + y ) = x ² – y ²). Исходя из h = (1 – √ 5 )/2, представим формулы Бине для чисел Фибоначчи и Люка в виде

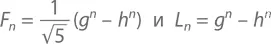
И когда мы их перемножаем, получается

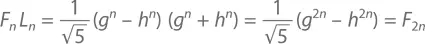
Откуда пришло название «золотое сечение»? Из золотого прямоугольника, в котором соотношение длинной и короткой сторон составляет g = 1,61803…

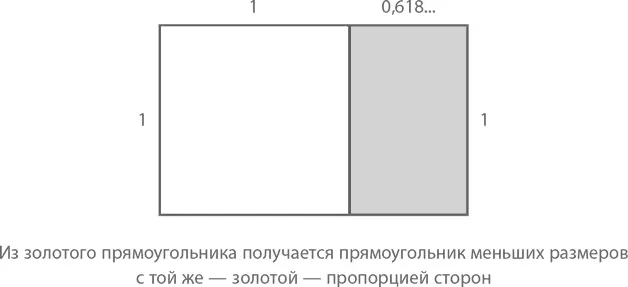
Если обозначить короткую сторону единицей и убрать из прямоугольника квадрат со сторонами 1 на 1, у нас останется еще один прямоугольник со сторонами 1 и ( g – 1), соотношение которых составит

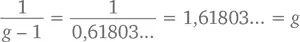
То есть пропорции маленького прямоугольника будут такими же, как и большого. Кстати, g – единственное в своем роде число со столь уникальными свойствами, потому что уравнение 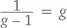подразумевает, что g ² – g – 1 = 0. А формула корней квадратного уравнения приводит нас только к одному положительному числу, удовлетворяющему этому условию, и число это – (1 + √ 5 )/2 = g .

Благодаря этому своему свойству золотой прямоугольник считается эстетически образцовым, а потому часто используется в разных областях искусства, будь то живопись, фотография или архитектура. Например, Лука Пачоли [14] – друг и соратник Леонардо да Винчи называл его «божественной пропорцией».

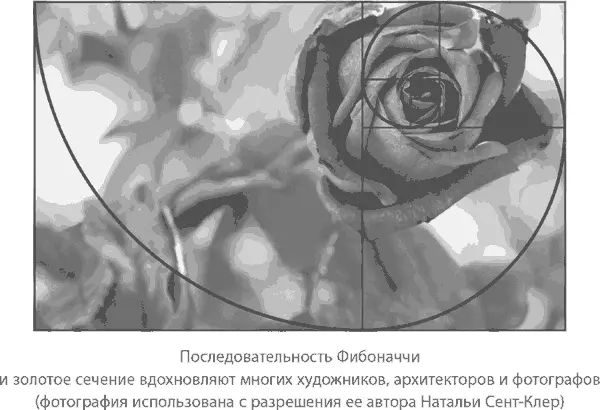
Золотое сечение лежит в основе стольких удивительных математических явлений, что подчас очень сложно удержаться от соблазна увидеть его даже там, где его нет и никогда не было. Например, в романе «Код да Винчи» Дэн Браун пишет, будто число 1,618 встречается везде и всегда, и подтверждение тому – строение человеческого тела, Браун утверждает, что отношение нашего роста к высоте, на которой расположен пупок, – 1,618. Я не проводил измерений, но в статье Джорджа Марковски «Выдумки о золотом сечении», опубликованной в журнале College Mathematics Journal , говорится, что это не соответствует реальности. Тем не менее каждый раз, когда где-то встречается число, хоть сколько-то близкое к 1,6, кто-нибудь вспоминает о золотом сечении.

Я уже не раз говорил, что многие числовые закономерности, в которых присутствуют числа Фибоначчи, суть настоящая поэзия. И это не просто метафора: эти числа действительно используются при создании стихотворений. Возьмем, к примеру, лимерики. Вот, последите за ритмом (пусть без слов, просто используя сетку слогов):

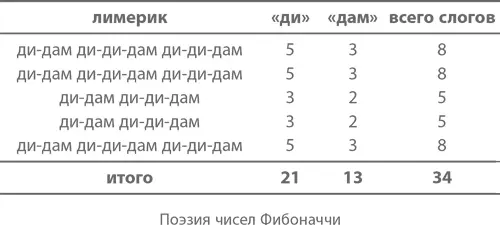
Если посчитать количество слогов в каждом ряду, мы получим числа Фибоначчи! Лично меня это вдохновило настолько, что я отважился написать о них свой собственный лимерик:

Одна из главных радостей занятий математикой – возможность окончательных, не оставляющих ни тени сомнения доказательств. Это ставит математику на особое место в ряду других наук, которые опираются на соответствие законам материального мира. Однако новые открытия могут опровергать или изменять эти законы. В математике же доказанное однажды остается доказанным навсегда. Прошло больше 2000 лет с того момента, как Евклид доказал бесконечность множества простых чисел – и это никогда не удастся оспорить. Научно-технические формации сменяют друг друга, теоремы же вечны. Как однажды сказал великий Годфри Харди [15]: «Математик так же, как художник или поэт, создает узоры. И если его узоры более устойчивы, то лишь потому, что они сотканы из идей». По-моему, доказать новую теорему – все равно что шагнуть на тропу, ведущую в научное бессмертие.

В математике доказывают не только абсолютную истинность, но и невозможность . Часто приходится слышать: «Нельзя доказать невозможное». Полагаю, здесь имеется в виду, что никому не под силу доказать существование розовых коров – по крайней мере, до тех пор, пока мы не увидим их в один прекрасный день. Но в математике невозможное вполне себе доказуемо . Например, сколько ни пытайтесь, вы ни за что не найдете два четных числа, которые в сумме давали бы нечетное. Или простое число, которое было бы больше всех остальных простых чисел. Сложность таких доказательств поначалу пугает, к ним нужно привыкнуть, и не ждите, что это произойдет с первого (а то и со второго или с третьего) раза. Но стоит войти во вкус – и удержаться уже невозможно: настолько они удивительны и притягательны. Стройное доказательство подобно хорошему анекдоту или уместной шутке – удовлетворение от него испытываешь ничуть не меньшее.

С вашего позволения, расскажу о первом своем опыте на этой стезе. В детстве двумя главными предметами моего обожания были настольные игры и загадки. Как-то раз мой друг предложил мне загадку, связанную с настольными играми, и, конечно, я был заинтригован. Он положил передо мной пустую шахматную доску размером 8 на 8 клеточек и 32 костяшки домино и спросил:

– Можешь выложить домино так, чтобы они закрыли всю доску?

– Конечно, – уверенно ответил я. – Просто по четыре костяшки на ряд. Вот так:

– Молодец, – сказал он. – А если я уберу две клетки – правую нижнюю и левую верхнюю, и их останется 62 – сможешь закрыть оставшиеся 31 костяшкой? – и он положил на крайние квадратики две монетки.