Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

Теорема:Если m и n – нечетные, то их произведение mn также будет нечетным.

Доказательство:Предположим, что m и n являются нечетными числами. Тогда m = 2 j + 1, а n = 2 k + 1 при целых значениях j и k . Тогда, согласно правилу FOIL,

А так как 2 jk + j + k – целое число, то mn есть форма «удвоенного целого числа + 1», а значит, нечетное число.◻

А что насчет обратного высказывания? Итак, если mn – нечетное, будут ли так же нечетными m и n ? Будут, и подтвердить это можно, используя доказательство от противного. Для этого нам нужно показать, что опровержение части «то…» (что m и n суть нечетные) приведет к ошибке, причем не только во второй, но и в первой части «если…». Что и подтвердит довольно странным, но вполне логичным образом наше предположение.

Теорема:Если mn – нечетное, то и m и n будут также нечетными.

Доказательство:Предположим, что либо m , либо n (или оба) – четные числа. Выберем m (хотя по большому счету это не важно). Значит, m = 2 j при целом значении j . Тогда произведение mn = 2 jn также получится четным, что противоречит изначальному условию.◻

В том случае, когда теорему можно доказать как в «прямом», так и в «обратном» порядке, ее иногда называют теоремой по принципу «если и только если» (или «тогда и только тогда»). Как раз такую мы сейчас и доказали:

Теорема: m and n являются нечетными, если и только если mn – нечетное («…тогда и только тогда, когда mn – нечетное»).

Возможно, теоремы, которые мы только что рассмотрели, ничем вас не удивили, а их доказательства показались вам весьма прямолинейными. Куда большее удовольствие получаешь, пытаясь подтвердить менее очевидные предположения. Пока что мы довольствовались целыми числами – не пора ли заняться дробями? Число, которое можно представить в дробном виде, называется рациональным. Если быть точным, то число r является рациональным, если r = a / b , где a и b – целые числа, а b ≠ 0. Например, 23/58, –22/7 или 42 (равное, по сути, 42/1) – числа рациональные. Если же число не является рациональным, его называют иррациональным. Яркий тому пример, о котором вы, наверняка, слышали – число π = 3,14159…, но о нем чуть позже, в главе 8.

Для следующей нашей теоремы не лишним будет вспомнить, как вообще складывать дроби. И легче всего это делать, когда дроби имеют общий знаменатель, например:

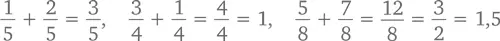
В противном случае нам сперва придется привести дроби к общему знаменателю:

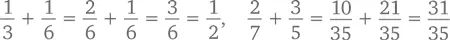
В целом же дроби a / b и c / d можно привести к общему знаменателю таким вот нехитрым способом:

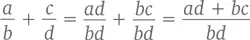
И этого вполне достаточно, чтобы доказать несколько простых теорем, связанных с рациональными числами.

Теорема:Среднее арифметическое двух рациональных чисел также будет рациональным числом.

Доказательство:Возьмем два рациональных числа – x и y . Значит, в равенствах x = a / b и y = c / d значения a, b, c и d суть целые числа. Среднее арифметическое x и y, таким образом, можно представить как

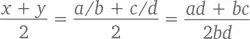
Это дробь, числитель и знаменатель которой – целые числа. Следовательно, среднее арифметическое значение x и y является рациональным числом.

А теперь давайте подумаем, что же именно утверждается в этой теореме. А утверждается в ней то, что между двумя разными рациональными числами, насколько бы близки они друг другу ни были, всегда найдется еще одно рациональное число. Возникает искушение сделать из этого вывод, что все числа являются рациональными (как довольно долго думали древние греки). Нет, это не так. И смотрите, почему. Возьмем число √ 2, которое в десятичной записи выглядит как 1,4142… Если мы попробуем записать его как обычную дробь, получится что-нибудь вроде 10/7 или 1414/1000 (вариантов огромное множество), но все они будут приблизительными и никогда при возведении в квадрат не дадут 2. Но что, если мы просто плохо ищем? Да нет, не плохо, и следующая наша теорема как раз и показывает, что любые такие поиски бесполезны по определению. Доказательство будет строиться от противного, как это обычно и бывает, когда разговор заходит об иррациональных числах. А заодно мы увидим, как сократить дробь до ее несократимого значения – того предела, когда у числителя и знаменателя остается только один общий делитель – 1.

Теорема:√ 2 есть иррациональное число.

Доказательство:Предположим обратное: √ 2 есть число рациональное. В таком случае существуют некие положительные целые числа a и b , для которых верно, что

где дробь a / b – несократимая. Возведя обе части уравнения в квадрат, получим

или

что приводит нас к тому, что a ² есть четное целое число. А если a ² – четное, значит, четным является и a (по аналогии с недавним нашим доказательством того, что, если нечетное a умножить на само себя, результат будет также нечетным). То есть a = 2 k , где k – целое число. Добавим это в свое уравнение и получим

То есть

что приводит нас к

и констатации того факта, что b ² является четным числом. Значит, четным должно быть и b . Но постойте! Ведь при четных значениях как a , так и b дробь a / b никак не может быть несократимой! Это противоречит нашим исходным условиям. И завело нас в эту ловушку предположение, что √ 2 является рациональным числом. Поэтому нам не остается ничего иного, кроме как признать: число √ 2 – иррациональное.☺