Артур Бенджамин - Магия математики: Как найти x и зачем это нужно

Мы видим, что сумма самого первого нечетного числа – 1 – и в самом деле составляет 1², то есть для n = 1 наше предположение абсолютно верно. Дальше нам следует обратить внимание на то, что, если сумма первых k нечетных чисел составляет k ², а именно

при добавлении следующего нечетного числа (2 k + 1) у нас получится

Другими словами, если сумма первых k нечетных чисел равна k ², то сумма первых k + 1 нечетных чисел обязательно будет равна ( k + 1)². Значит, теорема, истинная в отношении n = 1, будет столь же истинной в отношении любого значения n .◻

Индукция – инструмент действенный. Эта книга начиналась с проблемы определения суммы первых n чисел. Разными путями мы пришли к тому, что

Это предположение, безусловно, правдиво при n = 1 (потому что 1 = 1(2)/2). Предположим, что оно правдиво и для числа k :

Тогда, прибавив к этой сумме ( k + 1), получим

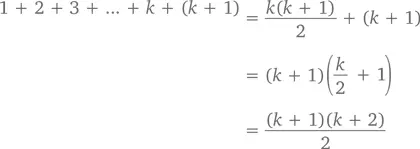
В этой формуле k + 1 использовано вместо n . Значит, если она верна для n = k (где под k может скрываться любое положительное число), она будет так же верна и для n = k + 1. Равно как и для любого положительного значения n .◻

В этой главе (да и в книге вообще) будет еще много примеров использования индуктивного метода. А пока для закрепления материала вот вам песня, написанная «музыкантами от математики» Дэйном Кэмпом и Ларри Лессером на мотив знаменитой «Blowin' in the Wind» Боба Дилана.

В главе 5 мы рассмотрели несколько задач, основанных на числах последовательности Фибоначчи. Попробуем доказать парочку из них, используя метод индукции.

Теорема:Для n ≥ 1

Доказательство (методом индукции):Если n = 1, то F 1= F 3 – 1, что соответствует 1 = 2 – 1, что безусловно истинно. Применим это к n = k , то есть

Добавив к обеим частям число Фибоначчи F k +1, получим

что и требовалось доказать.

Столь же простым будет доказательство для суммы квадратов чисел Фибоначчи.

Теорема:Для n ≥ 1

Доказательство (методом индукции):Если n = 1, то F 1² = F 1 F 2, что верно потому, что F 2= F 1= 1. Применив это к n = k , получаем

А теперь добавим к обеим сторонам F ² k+1:

что и требовалось доказать.

В главе 1 мы выяснили, что сумма кубов равна квадрату суммы, то есть

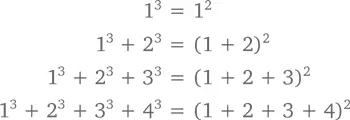
но тогда мы не были готовы это доказать. Просто мы ничего не знали об индукции. При n ≥ 1 общая закономерность выглядит так:

А так как нам уже известно, что 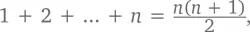докажем схожую теорему.

Теорема:Для n ≥ 1

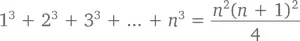
Доказательство (методом индукции):При n = 1 предположим, что 1³ = 1²(2²)/4, что истинно. Следовательно, если схожее предположение будет истинным и при n = k , теорема будет доказана:

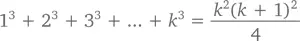
Прибавим к обеим сторонам ( k + 1)³ и получим

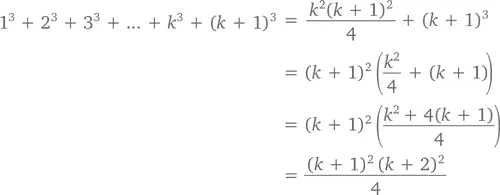
что и требовалось доказать.

А вот геометрическое доказательство тождества суммы кубов.

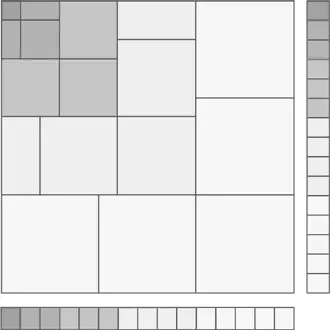
Посчитаем площадь фигуры двумя разными способами, а потом сравним результаты. С одной стороны, перед нами явно квадрат, каждая из сторон которого равна 1 + 2 + 3 + 4 + 5, а общая площадь, таким образом, – (1 + 2 + 3 + 4 + 5)².

С другой стороны, если начать с верхнего левого угла, а затем двигаться вниз по диагонали, мы пройдем последовательно через один квадрат размером 1 на 1, два размером 2 на 2 (один из которых разбит на два прямоугольника), три квадрата размером 3 на 3, четыре размером 4 на 4 (и еще один «разрезанный» пополам) и, наконец, пять квадратов размером 5 на 5. Следовательно, их общая площадь будет равна