Александр Волков - Артиллерия

Теперь нужно нанести обнаруженную цель на карту. Это поможет командиру батареи быстрее и точнее рассчитать по карте все данные для стрельбы по цели.

Измеренный вами на местности угол между ориентиром и целью вы отложите на карте при помощи прибора, без которого не может обойтись в бою ни один командир–артиллерист. Прибор этот – целлулоидный круг (рис. 222). Он служит для измерения и построения углов на карте. Изготовлен он из прозрачного целлулоида. Если такой круг наложить на карту, то сквозь него будут видны все отметки и топографические знаки, имеющиеся на карте, что очень важно.

Края круга с двух сторон срезаны. Это сделано для того, чтобы круг можно было свободно уложить в полевую сумку.

Окружность целлулоидного круга разделена на 600 равных частей (делений). Цена одного такого деления 0–10, или 10 "тысячных". Строить и измерять углы при помощи круга можно с точностью до 1/2 деления, то есть до 5 "тысячных".

Деления на окружности круга обозначены двумя рядами цифр через 1–00, при этом в одном ряду цифры идут по направлению движения часовой стрелки, а в другом ряду – в обратном направлении. Это облегчает отсчитывать и строить углы в обе стороны – влево и вправо.

На рис. 223 показано, как нужно при помощи целлулоидного круга наносить цель на карту, если известны две величины – угол от ориентира (1–20) и дальность (1700 метров). Прежде всего вы прочерчиваете на карте линию от точки своего стояния (НП) в направлении на ориентир. Затем вы накладываете целлулоидный круг на карту так, чтобы центр его совпал с точкой вашего стояния, а диаметр круга, обозначенный делениями 30 и 0, совпал с прочерченной линией. По шкале круга вы отсчитываете влево от ориентира угол 1–20. Это будет одно большое деление и два маленьких. Против деления, отвечающего отсчитанному углу, вы ставите на карте точку и, сняв с карты целлулоидный круг, проводите от точки стояния через наколотую точку прямую линию. На этой линии должна находиться цель. Отметить ее положение на карте уже нетрудно. Надо только в направлении прочерченной линии отложить от точки НП известное расстояние до дели 1700 метров (в масштабе карты) и наколоть соответственно этому расстоянию точку. Это можно сделать при помощи целлулоидного треугольника, на котором нанесена шкала дальности, "ли при помощи обыкновенной миллиметровой линейки.

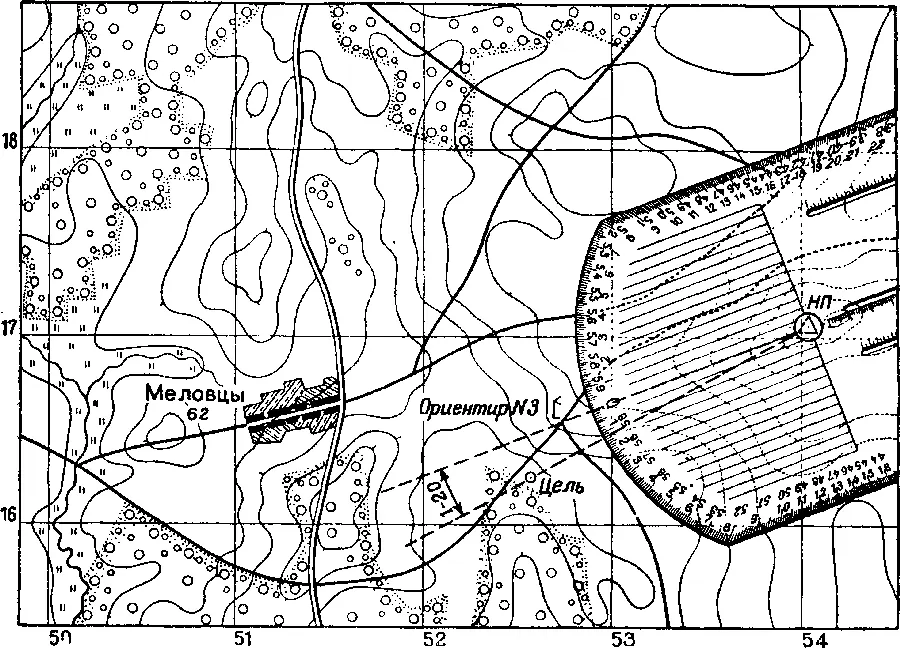
Рис. 223. Пользуясь целлулоидным кругом и треугольником или линейкой, вы можете нанести цель на карту

Понятно, что такой способ нанесения цели на карту дает достаточную точность только при условии, если дальность до цели определена точно и ориентир, относительно которого вы определяете положение цели, точно обозначен на карте.

Итак, цель на карту нанесена. Теперь остается лишь определить прямоугольные координаты цели, то есть положение ее в пределах квадрата карты. В нашем примере (см. рис. 223} цель находится в квадрате, который обозначен цифрами на полях карты – слева 16 и снизу 52.

Наложив на карту координатную мерку круга, как показано на рис. 224, вы определяете по ней расстояние до цели сначала от нижней стороны квадрата (вверх по оси X) и затем – от левой стороны квадрата (вправо по оси Y). Как видно из рис. 224, координаты цели будут: x=16 250 и у = 52 575. Первые две цифры в каждом из этих чисел относятся к номеру квадрата, а последние три цифры означают расстояния в, метрах от сторон квадрата.

Найденные координаты записываются в журнал целей. По этим координатам при помощи той же координатной мерки, если потребуется, можно нанести цель на другую такую же карту или огневой планшет, не производя уже никаких построений. Для этого нужно наложить координатную мерку на соответствующий квадрат карты (планшета) так, чтобы горизонтальная шкала мерки совпадала с нижней стороной квадрата и расстояние от угла мерки до левой стороны квадрата соответствовало 575 метрам, как это было показано на рис. 224. Очевидно, что цель будет находиться на срезе вертикальной шкалы координатной мерки против деления, соответствующего 250 метрам.

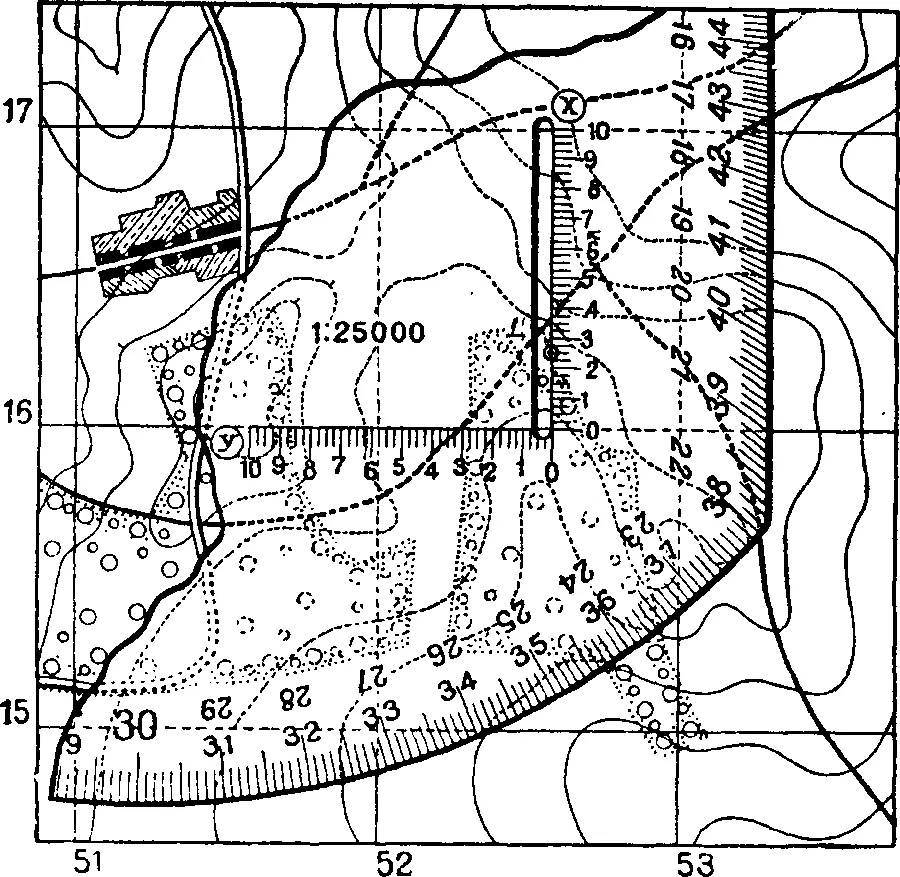
Рис. 224. Пользуясь координатной меркой целлулоидного круга, можно определить координаты цели

При глазомерном способе определения дальности нельзя рассчитывать на то, что местоположение цели будет определено совершенно точно.

Углы, правда, удается измерить с очень большой точностью: тут помогает нам такой совершенный оптический прибор, как стереотруба. Зато определение дальности до цели на глаз неизбежно сопровождается ошибкой, которая в среднем равна 10% измеряемой дальности.

Очевидно, что глазомерный способ определения дальности до цели не может нас вполне удовлетворить. Поэтому нам надо познакомиться еще с одним более точным способом.

Известно, что мы обладаем способностью на небольших расстояниях чувствовать удаленность предметов от наших глаз по усилию мышц, поворачивающих глаза в стороны. Чем сильнее приходится нам сводить глаза, тем ближе к нам находится предмет.

Очевидно, такое определение дальности, основанное не на математическом вычислении, а на ощущении, не отличается особой точностью. Но если бы мы даже и могли при взгляде на предмет измерять углы поворота глаз с точностью до одной "тысячной", все равно при определении дальности у нас получались бы значительные ошибки; слишком уж мало расстояние между глазами, оно равно всего–навсего 6–7 сантиметрам.

Другое дело, если бы мы могли раздвинуть наши глаза на метры или даже на километры: тогда точность определения расстояний этим приемом повысилась бы во много раз.

Этого именно и достигают при сопряженном наблюдении. Роль пары глаз берут на себя два наблюдательных пункта. Они располагаются на точно отмеренном или определенном по карте расстоянии в 1–2 километра один от другого. Это расстояние называется базой сопряженного наблюдения.

Наблюдатели обоих пунктов наводят свои стереотрубы друг в друга,, точно по направлению базы, на которой они расположены. Затем оба "глаза", и правый и левый, то есть оба наблюдателя, направляют стереотрубы на цель. При этом каждый записывает, на какой угол пришлось ему повернуть трубу от базы, чтобы увидеть цель. Все эти данные изображают затем на чертеже (на планшете). Получается схема, показанная на рис. 225.

Ясно, что цель окажется в точке пересечения обеих линий, показывающих направление "взгляда" того и другого наблюдателя.

Таким образом, местоположение цели будет определено на планшете. Остается теперь по этим данным вычислить дальность от орудия до цели в метрах. Это сделать уже нетрудно, так как на планшет артиллеристы наносят не только базу сопряженного наблюдения и засеченную: ими цель, но и точку, где стоит орудие (батарея). Все вычерчиваете" в одном масштабе. Значит, достаточно приложить масштабную линейку к точкам цели и орудия, чтобы узнать дальность до цели.