Анри Рухадзе - События и люди. Издание пятое, исправленное и дополненное.

Первым, кто понял необходимость описания плазмы с помощью кинетического уравнения, был Л. Д. Ландау. В 1937 году (ЖЭТФ, 1937) он обратил внимание, что условие газовости (1) в случае плазмы не выполняется, поскольку характерный радиус взаимодействия между частицами в плазме — радиус Дебая — намного больше среднего расстояния между частицами, т. е. имеет место обратное (1) неравенство

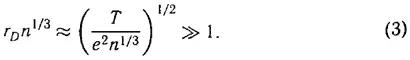
Здесь e — заряд частицы, а T — температура плазмы. Но условие (2) гласит, что средняя потенциальная энергия взаимодействия между заряженными частицами намного меньше средней кинетической (тепловой) их энергии, т. е.

что эквивалентно неравенству (3). Именно это условие ввел как условие газовости для плазмы Л. Д. Ландау.

Однако следующий шаг, который он сделал, а именно пошел по пути Л. Больцмана и записал уравнение Больцмана (уравнение Лиувилля с учетом парных столкновений) для плазмы как газа заряженных частиц, был, строго говоря, неверным. При этом он мастерски расправился с известной кулоновской расходимостью — записал конечный интеграл кулоновских столкновений, введя этом знаменитый кулоновский логарифм (по существу, логарифм обратного газового параметра η , см. (3')).

Буквально через год в цитированной выше статье А. А. Власов публикует свое знаменитое уравнение с самосогласованным полем, аргументируя его буквально теми же словами, что и Л. Д. Ландау. Именно, в сфере взаимодействия должно быть много частиц, т. е. выполняется условие (3). Но далее следуют совсем другие слова. Раз так, следуя рассуждениям А. А. Власова, то каждая частица в первом приближении взаимодействует сразу со всеми частицами, или, другими словами, с электромагнитным полем, создаваемыми всеми частицами плазмы. В результате в первом приближении мы имеем систему уравнений, состоящую из кинетического уравнения Лиувилля, в котором в качестве силы фигурирует сила Лоренца, и уравнения Максвелла для полей, соответствующих силе Лоренца. Источниками же полей в уравнениях Максвелла являются плотности зарядов и токов, создаваемых всеми заряженными частицами плазмы. Это и есть система уравнений Власова-Максвелла, или уравнения с самосогласованным полем.

А как быть дальше, как записать уравнения с учетом следующего порядка? Этот вопрос волнует Н. Н. Боголюбова и является предметом жарких споров его с А. А. Власовым в начале 1940-х годов в университетской аудитории на Моховой улице в Москве, куда несколько раз приезжал Н. Н. Боголюбов из Киева. Результатом горячих дискуссий Н. Н. Боголюбова и А. А. Власова и явилась упомянутая выше монография Н. Н. Боголюбова. В этой монографии он впервые применяет квантово-электродинамический метод в статистической физике. Н. Н. Боголюбов исходит из гамильтониана, состоящего из суммы гамильтонианов свободных частиц, поля и взаимодействия между ними (и только). Применяя к своей знаменитой цепочке уравнений для корреляционных функций теорию возмущений (разложение по степеням е 2 ), он получает в первом приближении по е 2 кинетическое уравнение Власова, а в следующем приближении (с точностью до е 4 ) — уравнение Власова с интегралом столкновений Ландау. Этим был завершен последовательный вывод кинетических уравнений для газов Н. Н. Боголюбовым. Но почему-то этот метод известен как метод ББГК (Боголюбова-Бома-Гросса-Крука). Хотя работы последних трех ученых появились независимо, однако несколько позже!

И уже значительно позже, когда квантовая электродинамика была создана, Р. Балеску, используя метод фейнмановских диаграмм, показал:

1) при учете только вершинной диаграммы (частица излучает или поглощает поле) получается уравнение Власова;

2) при учете наряду с вершинной диаграммой также и обменной диаграммы (одна частица излучает поле, а вторая его поглощает) — уравнение Власова с интегралом столкновений Ландау;

3) а просуммировав все пересекающиеся обменные диаграммы («лестничное» приближение), придем к уравнению Власова с интегралом столкновений Ленарда-Балеску (с учетом поляризации плазмы при взаимодействии частиц).

Таким образом, систему уравнений для описания кинетики плазмы с полным основанием следовало бы назвать системой Власова-Ландау-Боголюбова-Максвелла (в порядке возрастания вклада каждого в физику в целом).

Познакомился с Яковом Борисовичем я в мае 1959 года, в Харькове, куда приехал на конференцию по физике плазмы вместе со своим учителем В. П. Силиным. Познакомил нас ставший сегодня легендарным Александр Ильич Ахиезер. Тогда же мы с Виктором Павловичем познакомились и с другими учениками Александра Ильича: К. Н. Степановым, А. Г. Ситенко, В. Г. Барьяхтаром, С. В. Пелетминским и другими. Очень скоро наши отношения с последними стали дружескими, и это продолжается до сих пор. Что же касается моих отношений с Яковом Борисовичем, то они были не дружескими, а скорее сродни отношениям ученика с учителем. Да, я ему обязан выбором научного направления, которое стало делом всей моей жизни. Тогда я уже знал знаменитую работу Александра Ильича и Якова Борисовича по резонансной плазменно-пучковой неустойчивости, которая резонансно возбудила и на всю жизнь зарядила меня. И не случайно подавляющее большинство моих работ начинается со ссылки на эту работу Александра Ильича и Якова Борисовича. Тогда же я привес в Харьков на обсуждение работу, выполненную мною совместно с Л. М. Коврижных, по нерезонансной неустойчивости бесстолкновительной плазмы с током, сегодня известной как бунемановская неустойчивость. Работа О. Бунемана была опубликована в 15-м томе «Physical Review» 1959 года, но стала известной у нас в стране только во второй половине 1959 года. Яков Борисович в мае 1959 года ее еще не знал. А он следил за литературой, как никто другой, и всегда был в курсе всех публикаций раньше других. Его поразительная осведомленность всегда восхищала меня. Так или иначе, но, окрыленный его одобрением нашей работы по приезде в Москву, я сразу послал статью в «ЖЭТФ». Статья была опубликована в третьем номере 35-го тома «ЖЭТФ» за 1960 год (поступила в редакцию 4 июля 1959 года) и в ней ссылок на работу О. Бунемана, естественно, нет. Так началась наша дружба с Я. Б., так зародилась моя любовь к черенковским плазменно-пучковым неустойчивостям. И этот мой выбор был определен Яковым Борисовичем. Наша дружба еще больше укрепилась в 1964 году, когда Яков Борисович согласился быть моим оппонентом по докторской диссертации и дал очень хороший и теплый отзыв. И это понятно, половина диссертации была посвящена пучковым неустойчивостям и, по существу, представляла собой оду пионерским работам Якова Борисовича. Яков Борисович редко выезжал из Харькова, хотя и часто бывал оппонентом. И я горжусь тем, что на мою защиту в холодный мартовский день он приехал. Вот так.