Анри Рухадзе - События и люди. Издание пятое, исправленное и дополненное.

откуда следует, что ζ действительно растет с увеличением времени релаксации τ .

С. П. Дьяков в 1954 г. показал [6], что формула (2) и условие ее выполнения могут быть эффективно использованы для определения структуры и ширины слабых ударных волн в сильно релаксирующих средах. Действительно, в соответствии с гидродинамической теорией ударных волн [1] давление в переходном слое слабой ударной волны (т. е. ее структура) определяется в соответствии с законом

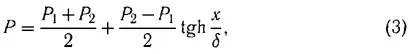
где x — пространственная координата, P 1, P 2 — давление соответственно впереди и за фронтом волны, а δ — ее ширина, определяемая формулой

где V, S — удельные объем и энтропия, ∆ P = P 1 — P 2 — перепад давления в ударной волне, а

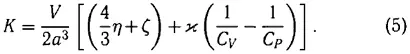
В формуле (5) a, C V, C P — скорость звука и удельные теплоемкости при постоянных давлении и объеме, а все входящие а правую часть (4) величины (кроме ∆ P ) относятся к состоянию перед волной. С. П. Дьяковым было замечено, что поскольку в силу (4) ширина переходного слоя ударной волны обратно пропорциональна ее амплитуде, то для достаточно слабых ударных волн в редактирующей среде состояние вещества в переходном слое можно считать изменяющимся медленно по отношению к установлению равновесия, что позволяет трактовать процесс релаксации в духе метода Мандельштама-Леонтовича с использованием выражения (2) в (5), пренебрегая при этом теплопроводностью и обычной вязкостью. В результате была получена формула

возможность пользования которой требовала установления еще условия медленного изменения состояния вещества в переходном слое. Сформулированное в общем виде δ >> a 0 τ , в силу (2) и (6) это условие было конкретизировано в форме общеизвестного ныне критерия

Описанный выше метод нашел приложение для некоторых важных классов релаксирующих систем [7–9] и в настоящее время широко известен как «метод концепции второй вязкости Мандельштама-Леонтовича-Дьякова».

Как уже отмечалось выше, проблема устойчивости фронта ударной волны вновь стала в центре внимания исследователей с начала 1970 г., когда это явление получило подтверждение экспериментом, а работа Сергея Петровича [2] — дальнейшее развитие. Ряд обобщений и идей в этой области принадлежит О. А. Синкевичу, которому мы и предоставим слово.

— В настоящее время становится очевидным, что именно механизм устойчивости обеспечивает отбор различных эволюционирующих состояний в живой и неживой природе. Если останавливаться только на неустойчивостях в распределенных системах, то во многих случаях можно выделить неустойчивости, вызванные внутренними состояниями и процессами в среде, и неустойчивости, обусловленные активными границами.

С. П. Дьяков был одним из первых, кто убедительно продемонстрировал роль активных границ в задаче об устойчивости плоских ударных волн с произвольным видом ударной адиабаты Гюгонио P = P ( V ) H (здесь P — давление, V = 1/ ρ — удельный объем, а ρ — соответственно плотность среды) относительно двумерных гофрировочных возмущений. Для плоской ударной волны, распространяющейся в положительном направлении оси y , когда невозмущенная плоская поверхность фронта совпадает с плоскостью x0y , Сергей Петрович исследовал в линейном приближении устойчивость первоначально малых возмущений ξ (вязкостью и теплопроводностью пренебрегалось) вида ξ ~ exp(ikx — iωt). Поскольку ударная волна движется со сверхзвуковой скоростью относительно газа перед фронтом волны, то, естественно, возмущения туда не проникают. Для линеаризованных уравнений газодинамики выбирались следующие граничные условия: ограниченность возмущений при z → ∞ и соотношения на фронте ударной волны, вытекающие из обычных законов сохранения потоков массы, импульса и энергии. Полагая произвольной форму ударной адиабаты, выделяя возмущения в энтропийновихревой и звуковой волнах, С. П. Дьяков из решения характеристического уравнения получил условия неустойчивости плоской ударной волны относительно гофрировочных возмущений в виде

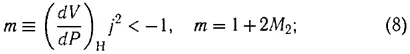
здесь j = ρ 1v 1= ρ 2v 2 — поток массы через фронт ударной волны, M 2= V 2/a S2 — число Маха, v 2 — скорость среды за фронтом, a S2 — скорость звука за фронтом ударной волны, (dV/dP) H — производная от ударной адиабаты, индексы 1 и 2 относятся соответственно к состояниям перед фронтом и за фронтом ударной волны.

Кроме условий (8) неустойчивости ударной волны С. П. Дьяков установил, что в области параметров, удовлетворяющих условию

где

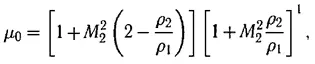
существуют решения с незатухающими возмущениями фронта волны (стационарными в некоторой системе координат, скользящей вдоль фронта), к которому со стороны зафронтового течения примыкают звуковые волны, исходящие под определенным углом. Область параметров

была отнесена С. П. Дьяковым к области устойчивости плоских ударных волн относительно малых гофрировочных возмущений.

Последующие многочисленные исследования устойчивости плоских ударных волн [10–11], выполненные различными методами, не изменили границ области возникновения неустойчивости (8). Учет вязкости и теплопроводности газа [14, 15] также не изменили положение границ области (8). Однако уточнения нижней границы области (9), проведенные в работах {9-12, 16], показали, что

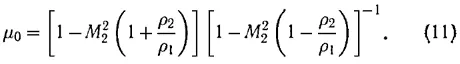
Дальнейший, более детальный анализ характера проведения малых возмущений показал, что в устойчивой области, если не учитывать вязкость и теплопроводность газа, возмущения ударной волны могут затухать во времени по степенному закону t -3/2 (возмущения в сильной ударной волне затухают по закону t -1/2 ). Учет конечной вязкости [13] или конечной проводимости среды за фронтом ударной волны, движущейся в поперечном магнитном поле, может приводить к экспоненциальному затуханию возмущений и к исчезновению области спонтанной генерации звука [19, 20].