Аркадий Велюров - Пепелацы летят на Луну. Большой космический обман США. Часть 10

Vк»= Vк + Vземля конечная скорость с учетом вращения Земли. Ну а теперь сам запуск «Аполлон-12». Я сейчас в руках держу документ. Здесь написано: «весовая сводка Сатурн—5 Аполлон—12 (в кг)». Источник информации (1) файл в каталоге 4—12. Здесь описана вся короткая жизнь изделия Сатурн—5 с момента команды «зажигания», а до отделения корабля от носителя. В конце написана магическая фраза: «Эти данные могут использоваться при всех анализах весов Сатурн—5». Раз написано всех, то мы именно так и сделаем. (Данные в таблице округлены до целых кг.). Весовая сводка Saturn V Apollо-12 (кг).

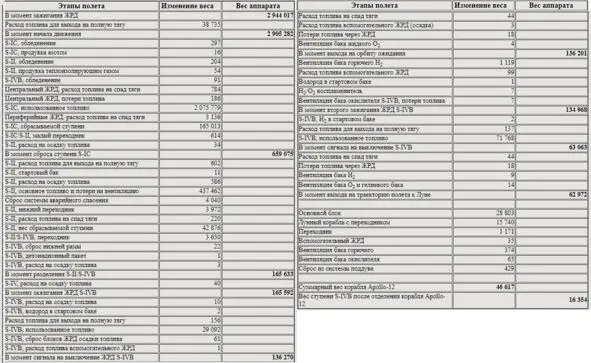
Для начала найдем суммарную идеальную скорость всех ступеней «Сатурн-5». Масса в момент отрыва от стола ≈2905,3 т. Расход топлива включая период падения тяги ≈2080,0 т; тогда Z1= 2905,3/ (2905,3—2080,0) =3,52; при I=2982 м/с Vx1=I*Ln (Z1) ≈3753 м/с; остаточная масса ступени с остатками топлива Мк1≈165 т. Вскоре после разделения ступеней, идет отделение всякого балласта: САС ≈4 т и переходника между ступенями весом: 3972 кг+614 кг+34 кг+11 кг+586 кг≈5,2 т.

Для упрощения расчетов будем считать, что все эти разделения происходят одновременно. Так как эти 9,2 т сбрасываются почти сразу после разделения, то их влияние на дальнейший полет минимально По существу их можно методически добавить к Мк1 ≈174,2 т. Фактически расход топлива через двигатели второй ступени ≈438,3 т; остаточная масса ступени с недобором топлива и переходником Мк2 ≈46,6 т; с учетом массы третьей ступени с кораблем Аполлон в момент разделения ~165,6 т имеем общую массу в начале работы второй ступени ≈650,5 т. тогда Z2=650,5/ (650,5—438,3) ≈3,065 Vx2 ≈4668 м/с при I=4168 м/с (отношение компонентов 5,5:1). Масса комплекса перед первым включением третей ступени = 165,6 тонн; расход через двигатель фактически 29,3 т. топлива при первом импульсе третьей ступени; тогда Z3 = 165,6/ (165,6—29,3) ≈1,215; Vx3 ≈823 м/с при I=4227 м/с (отношение компонентов 4,5:1).

После этих операций оставшаяся масса комплекса ~136,3 тонны является искусственным спутником Земли. Это удобно тем, что нам заранее известен конечный результат: Vк ≈7790 м/с. Именно такова скорость спутника на круговой орбите высотой ~190 км. Условием выведения спутника на круговую орбиту есть достижение указанной скорости на высоте 190 км при нулевом угле тангажа. Прибавку скорости из-за вращения Земли будем считать Vземл≈465*cos (φ) *sin (A) где А-азимут пуска и φ – широта старта (465 м/с – линейная скорость точки на экваторе), то тогда при типичных значениях А=72º и φ=28,3º имеем Vземл≈390 м/с. Итак, будем считать (грубо) прибавку за счет вращения Земли 390 м/с. Отсюда можем прикинуть величину действительных потерь скорости Х на участке выведения ИСЗ:

3753+4668+823-Х+390=7790 м/с.

Тогда Х=1844 м/с. Обобщая разброс параметров, можно показать, что для ракеты Сатурн-5 допустимо принять стандарт потерь первой фазы полета: Х≈1850±50 м/сек

Масса объекта перед вторым включением третей ступени = 134,9 тонн. Эта масса стала меньше на примерно ~1,2 т главным образом за счет утечки водорода через дренаж; остаток топлива по факту = 71,9 тонн, тогда Z4 =134,9/ (134,9—71,9) ≈2,141; теоретический размер импульса Vx≈3218 м/с при I =4227 м/с. Как видим, ракета Сатурн-5 располагает запасом полной характеристической скорости Vx≈12460 м/с. Согласно данных НАСА, все отправляющиеся к Луне корабли имели скорость в конце орбитального разгонного импульса ~10840 м/сек. Это значит, что полные совокупные потери, с учетом потерь на второй импульс с промежуточной орбиты ожидания, составляют Хп≈2000±50 м/сек. Из них ~1850 м/с мы потеряли на вывод на промежуточную орбиту ИСЗ. Так что потери второй фазы полета ~150 м/с.

Итоговая масса полезной нагрузки 46,6 тонн, включая переходник=1,17 т.; масса вместе с последней ступенью равна ~63,0 тонн. Масса последней ступени, включая недобор топлива 16,4 т; чистая масса корабля Аполлон ~44,5 т. Именно такой груз далее следует по высокоэллиптической орбите к Луне. Хронология запусков Сатурн-V. Их было всего 13 в период 1967—73 гг. Ура, товарищи! Тем, кто уже уснул – очнитесь. Выше был приведен полный расклад, и все цифры, как говорится, сошлись до копейки. Короче мы героически отправили к Луне потребные 44,5 тонн по нашей методике. Это и есть тот самый эталонный расчет эталонного носителя вместе с эталонным кораблем, который к месту и не к месту с искажениями и интерпретациями гуляет по разным источникам. Надо отдать должное умным головам из НАСА – формулы Циолковского они знают (когда надо) и все у них сходится, хоть запускай налоговых ревизоров делать контрольную закупку. От себя добавлю, что проблемы с цифрами у них возникают именно тогда и там, где целью полета не является высадка людей на поверхность Луны. Ненадолго пошлем всех этих американцев на… Луну.

Перенесемся в 1973 год в май месяц 14 число. В этот день двухступенчатый вариант ракеты Сатурн-5 вывела на орбиту с наклонением в 50º и высотой 427х439 километров груз весом 74783 кг. На фотографии: «Скайлеб» с одним «крылом». Левое «крыло» потеряли. Подробное описание таково: «Skylab 1 Nation: USA. Program: Skylab. Payload: Skylab Orbital Workshop. Mass: 74,783 kg. Class: Manned. Type: Space station. Spacecraft: Skylab, Apollo ATM. Agency: NASA MSF. Perigee: 427 km. Apogee: 439 km. Inclination: 50.0 deg. Period: 93.2 min. COSPAR: 1973—027A. USAF Sat Cat: 6633. Decay Date: 11 July 1979».

Далее я решил задаться посторонней задачей: сколько груза может вывести двухступенчатый вариант РН Сатурн-5 на опорную орбиту ИСЗ высотой 450 км и наклонением 50º? Считаем. Для начала нам нужно выяснить, насколько полная идеальная скорость для вывода на орбиту высотой H₂=450 км должна быть больше, чем полная идеальная скорость при выводе на орбиту высотой H₁=190 км. Пусть у нас есть тело единичной массы на низкой орбите H₁. Тогда запишем закон сохранения энергии:

V²/2 – μ/R = C

Здесь μ – гравитационный потенциал Земли, равный 3,986×10 14; R – расстояние до центра Земли R=Ro+H₁; Ro=6378 км.

Пусть V₁ – круговая скорость на высоте H₁

и V₂ – круговая скорость на высоте H₂

При подъеме с высоты H₁ до высоты H₂ происходит увеличение потенциальной энергии спутника

ΔEп=μ/R₁ – μ/R₂. Что приводит к уменьшению, соответственно, кинетической энергии ΔЕк.

Нам необходимо такое превышение кинетической энергии ΔEк спутника на высоте H₁, чтобы поднимаясь вверх до высоты H₂ против сил тяжести, наша кинетическая энергия после подъема была бы:

Ек = V²/2 ≥ (V₂) ²/2.

Тогда искомая скорость Vx на высоте H₁ равна:

Vx² = (V₂) ² +2*ΔEп = (V₂) ²+2μ (1/R₁ – 1/R₂); ΔV=Vx —V₁;

Если H₁=190 км; V₁ =7790 м/c; H₂=450 км; V₂=7640 м/с;