Аркадий Велюров - Пепелацы летят на Луну. Большой космический обман США. Часть 10

Хорошо, давайте внимательно изучим личность этого самого Вернера фон Брауна. Вот его послужной список: С 1933 г. Вернер фон Браун носил черную форму 4-го кавалерийского эскадрона 6-го полка СС. 24 декабря 1944 г. Гитлер наградил Вернера фон Брауна «рыцарским крестом с мечами» – одним из высших нацистских орденов. Штурмбанфюрер СС. Член нацистской партии НСДАП. Тут уместно еще задаться одним вопросом: На каком основании правительство США укрывало члена преступной организации СС? Именно так трактует Нюрнбергский вердикт суда эту ситуацию. И еще появляется вопрос: Каким это образом респектабельная фирма НАСА решилась на сотрудничество с нацистскими преступниками?

Ссылки. Использованная литература:

1.Mark Wade, www.astronautix.com

2.«Космонавтика», Гл. редактор В. П. Глушко.

Изд. «Сов. Энциклопедия» М. 1970 г.

3.«Пилотируемые полеты на луну, конструкция и характеристики Saturn-V Apollo»

М., 1973 г. Серия «Ракетостроение», т. 3

http://www.epizodsspace.narod.ru/bibl/raketostr3/obl.html

4.«Баллистика летательных аппаратов»

Ю. Г. Сихарулидзе, М., 1982 г.

5.«Apollo 8: The First Lunar Voyage»

http://www.hq.nasa.gov/office/pao/History/SP-4205/ch11-6.html

6.В.И.Левантовский. «Механика космического полета»,

М., «Наука», ГРФМЛ, 1980

7.«Saturn 5 SA-501 launch vehicle flight evaluation report»

http://www.klabs.org/history/history_docs/jsc_t/apollo_04_technicalOinformation_summary.pdf

8.Использованы иллюстрации НАСА

http://history.nasa.gov/

Итак, дорогие читатели, в прошлой главе мы с Вами узнали о том, как не хорошо воровать водород у американского народа. Некоторые мои критики утверждают, что указанную недостачу, оказывается, покрывает железная болванка, запущенная в космос вместе с кораблем «Аполлон-8». Такое техническое решение потрясает своей простотой и изяществом, ибо ничто не сравнится с простой железной болванкой весом около 9 тонн! Тут я вынужден лишь развести руками: НАСА не имеет себе равных в сфере отправки балласта на Луну. Ниже, фотографии ступеней ракеты «Сатурн-5», слева направо: (первая) ступень S-1C; (вторая) ступень S-II; (третья) ступень S-IVB.

На самом деле, мои придирки к полету корабля Аполлон-8 носили, в сущности, мелочный характер. Какая, в сущности, разница: было ли украдено 22 тонн топлива, а может только 15 или вовсе 7. В конце концов, на любой нефтебазе Вам расскажут, как украсть бензин цистернами, поэтому американские шалости с бухгалтерией и статистикой выглядят вполне невинно. Все свои изыскания я проделал с единственной целью: показать насколько наш «подследственный» глупо врет и путается в деталях. Наглядный пример – при одинаковом импульсе, выданном двигателем третей ступени в сумме двух включений, в первом случае «Аполлон—4» увеличил апогей орбиты всего лишь до 17400 км, а во втором случае «Аполлон-8» совершил облет Луны с теми же данными. Любознательный читатель без труда поймет, что разница приращения скорости в этих маневрах полтора раза: ~2000 м/с и ~3000 м/с.

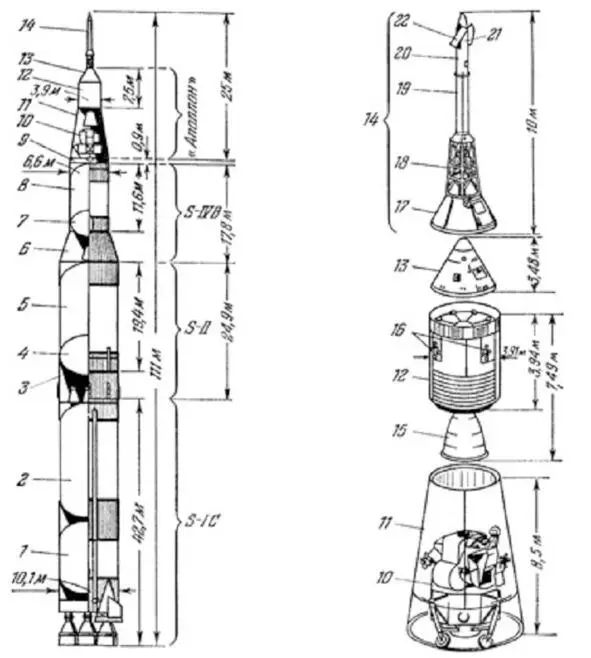
Для лучшего понимания проблемы представлена схема ракеты «Сатурн-5» из книге «специалиста» в области ракетостроения Шунейко И. И., выпускника сельскохозяйственного института: а) структура системы в целом; б) компоновка корабля «Аполлон». S-IC – первая ступень, S-II – вторая ступень, S-IVB – третья ступень; 1 – бак горючего первой ступени, 2 – бак окислителя первой ступени, 3 – переходник между первой и второй ступенями, 4 – бак окислителя второй ступени, 5 – бак горючего, 6 – переходник между второй и третьей ступенями, 7 – бак окислителя третьей ступени, 8 – бак горючего третьей ступени, 9 – приборный отсек IU, 10 – лунный отсек, 11 – переходник LMA, 12 – служебный отсек, 13 – командный отсек, 14 – система аварийного спасения (САС), 15 – маршевый двигатель служебного отсека, 16 – блоки двигателей системы ориентации и стабилизации, 17 – теплозащитный экран, 18 – ферма САС, 19 – основной РДТТ САС, 20 – РДТТ для отбрасывания САС, 21 – вспомогательный РДТТ, 22 – аэродинамические рули САС.

В следственных делах есть классическая фраза: в показаниях «подследственного» наметились противоречия, поэтому назначаем очную ставку. Далее мы сделаем виртуальную очную ставку между двумя хорошо описанными, а потому хорошо документированными событиями. Это запуск корабля «Аполлон—12» на Луну, и вывод на орбиту ИСЗ космической станции «Скайлеб». Для понимания всего дальнейшего, нам понадобится следующий математический аппарат.

Во-первых, формула Циолковского: ΔV=Iуд×Ln (Z);

где V – характеристическая скорость, I – удельный импульс двигателя, Z – отношение масс вначале и в конце работы двигателя. Во вторых, согласно методу характеристических скоростей для определения конечной скорости активного участка выведения существует следующее уравнение:

Vк=∑ (Vxi) —Vпотерь+Vземля=∑ (Ii*Ln (Zi)) —Vпотерь+Vземля;

Смысл этого равенства звучит так: конечная скорость Vк активного участка полета ракеты равна сумме характеристических скоростей всех ступеней минус константа (суммарный интеграл потерь скорости) + прибавка за счет вращения Земли. Интеграл потерь скорости на всем отрезке от 0 до Т есть некое конкретное число, грубо говоря, постоянное для данного типа ракеты. Этот вывод мы можем получить следующим образом. Для скоростной системы координат запишем дифференциальное уравнение:

m (dV/dt) =P*cosα – mg*sinβ – X

dV= [(P/m) *cosα – g*sinβ – X/m] dt

здесь Р – тяга ЖРД; Х – сопротивление воздуха; α – угол между вектором тяги Р и вектором скорости V;

β – угол вектора скорости к местному горизонту; расход топлива dm/dt = —L (масса убывает). Кроме того, P (h) =Pп – p (h) Sa = Pп (1- ph*γ) – высотная зависимость тяги от давления воздуха на данной высоте.

здесь ph=p (h) /po и γ= (Pп – Po) /Po, тогда

dV= (Pп/m – (Pп/m) * (1— cosα) – ph*γ*cosα * Pп/m – g* sinβ – X/m) dt

Начальные условия задачи V=0; H=0; m=M1

Конечные условия V=Vк; H=Hк; m=M2

Интегрируем по частям (вводя замену dt = – dm/L):

∫ (Pп /m) dt = – ∫ (Pп /mL) dm = (Pп /L) *Ln (M1/M2) = U*Ln (z) = Vхар. Это идеальная (характеристическая) скорость ракеты; U= Pп/L – удельный импульс в пустоте

z – отношение масс в начале и конце работы ЖРД

Суммарный интеграл потерь включает в себя четыре члена:

∫ (Pп/m) (1- cosα) dt = Vхар* (1- cosα) средние потери на управление

∫ (ph*γ*cosα * Pп/m) dt = Vхар* (ph*γ) средние потери на «высотность» ЖРД

∫ (g*sinβ) dt = T* (g*sinβ) средние потери гравитационные, здесь Т – время полета

∫ (X/m) dt потери на сопротивление воздуха.

Итого: Vк=Vхар – Vупр – Vду – Vграв – Vаэро

Данный вывод мы получили для случая одноступенчатой ракеты. Он легко обобщается на многоступенчатую ракету следующим образом: Vк=∑Vхар – ∑Vупр – ∑Vду – ∑Vграв – ∑Vаэро