Аркадий Велюров - Пепелацы летят на Луну. Большой космический обман США. Часть 10

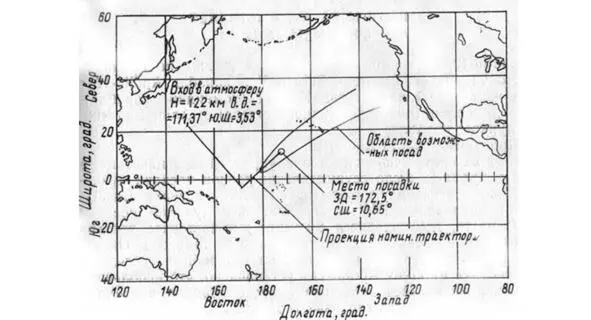
Рис.4: Место посадки командного отсека корабля «Apollo-11». Вопросы (риторические): Согласно данным [5] в Тихом океане было задействовано при всех полетах после «Apollo-11» два корабля службы спасения и поиска? Интересно, как всего двумя кораблями покрыть указанный на карте район поиска? И это при том, что в рядовых орбитальных полетах количество морских судов ВМФ США обычно в два-три раза больше. Корабли в Атлантике не в счет, до Атлантики «Apollo» точно не должен был дотянуть. Давайте рассчитаем условный перигей траектории Аполлонов. Если мы знаем параметры траектории для некоторой точки: Vвх, θвх, Hвх, то из системы уравнений:

(здесь r – радиус-вектор точки, r = ro+Hвх; μ – гравитационный параметр Земли)

r•v•cos (θ) =const – второй закон Кеплера;

v²/2 – μ/r =const – закон сохранения энергии;

Нам не известны vп и rп в точке перигея, но известно, что в точке перигея θперигей = 0

rвх • vвх • cos (θвх) =rп • vп

vвх²/2 – μ/rвх =vп²/2 – μ/rп

Далее система двух арифметических уравнений с двумя неизвестными сводится к квадратному уравнению:

rп² • (vвх²/2 – μ/rвх) + rп • μ – vвх² • rвх² • cos² (θ) /2 = 0

Дабы не отяжелять текст, приведу результат: для стандартного угла входа -6,5° на высоте ~120 км получаем перигей в районе ~36 м. И еще один момент нужно учесть. Нагрузка на мидель (площадь сечения перпендикулярного вектору скорости) у кораблей Аполлон и Зонд/Союз отличается в полтора раза: у Аполлона 5560 кг веса на 12 в.м. миделя, а у Союза – 2850 кг на 3,8 кв. м. миделя; т.е. у Аполлона «парусность» в полтора раза выше. Это означает, что аналогичные аэродинамические силы будут для него достигаться в несколько более высоких слоях атмосферы. Для того чтобы траектория спуска «Союза» и «Аполлона» имела одинаковый «профиль» с точки зрения аэродинамических сил, последний при равной скорости должен находится на высоте, где плотность воздуха в полтора раза меньше. Сделаем оценку параметра: пусть плотность атмосферы

ρ = ρ 0 • exp (– h / h 0); h 0= ~ 7170 м;

Тогда расстояние между высотой траектории «Союза» h 1 и «Аполлона» h 2

ρ 1 / ρ 2 = 1.5 = exp ((h 2 —h 1) /h 0); (h 2 —h 1) = 0.405 • h 0; (h 2 —h 1) = ~2,9 км;

Это означает, что средний профиль траектории Аполлона при прочих равных условиях, для достижения одинаковых перегрузок, должен быть выше на ~2,9 км. Итак, мы рассчитали параметры коридора входа для СА Аполлон как множество эллиптических орбит с перигеем в диапазоне от 44,9 км (42+2,9) до 58,9 км (56+2,9) при средней линии 51,9 км (49+2,9). В угловых параметрах для высоты 120 км наклон скорости к местному горизонту должен быть в диапазоне от 5,6° до —6,1°. К сожалению, «Аполлон» промахивался мимо коридора и шел ниже – в районе плюс-минус 36 км перигея или -6,5° угол входа. Ниже на рис. 5: «Skip range» – длина «прыжка»; «Ballistic trajectory» – внеатмосферный участок спуска. При управляемом спуске, с углами входа в атмосферу в рекомендуемом диапазоне, на траекторной линии есть точка, где вертикальная скорость Vy=0. Рис.5. Двойное погружение и прыжок, НАСА:

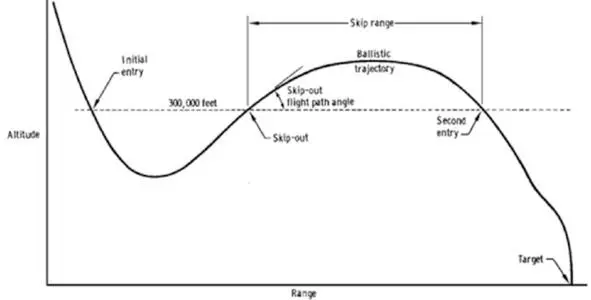
До этой точки вертикальная скорость отрицательная, капсула падает вниз, после этой точки вертикальная скорость положительная, начало восходящей ветви траектории. Назовем эту точку (условно) точкой рикошета. Горизонтальная скорость в этой точке примерно 8 км/с. Отметим, однако, что при слишком больших углах входа и при баллистическом спуске, такой точки может не быть, и вдоль всей траектории вертикальная скорость Vy будет отрицательной. Так вот, при меньших углах атаки эта точка расположена в более высоких слоях атмосферы. При больших углах входа эта точка будет находиться в нижних слоях атмосферы. Версия НАСА совсем другая.

Математически можно записать так: длина второго участка атмосферного спуска будет являться решением прямой задачи баллистики из начальной точки – точки рикошета, где Vy=0; при скорости бросания около 8 км/с; известной высоте точки «рикошета» Н р; при ненулевом аэродинамическом качестве K= Fy/Fx. Зная начальные параметры входа, и варьируя параметр K= Fy/Fx, мы можем влиять на дальность района приземления.

Поэтому длина траектории является важным косвенным признаком. Дальний рикошет говорит о малых углах входа и умеренных перегрузках, быстро «утонули» в атмосфере – большие углы входа и большие перегрузки. Численное моделирование на компьютере показывает, что при входе в секторе от -5,6° до -6,1° капсула Аполлона испытала бы максимальные перегрузки в пределах 4÷7 единиц с возможностью «прыжка» на расстояние 6000 км – 9000 км. А в случае срыва на баллистический спуск перегрузки не превысят 10÷11 единиц.

Если принять угол входа в районе -6,5°, то максимальные перегрузки, при управляемом спуске, достигнут ~9 g, при баллистическом спуске до ~16 g (примерно под таким углом входил «Зонд-5», так что данные численного расчета совпадают с данными конкретного полета). Для крайних случаев с максимальным углом входа -7,08°(«Аполлон-4») перегрузки составят ~12 g при управляемом спуске, и ~22 g на баллистике. Вопросам реализации численного моделирования спуска капсулы в атмосфере, и сравнению данных разных программ, а также табличным данным атмосферы я решил уделить специальное приложение.

Приложение: «Как „Аполлоны“ спускались в атмосфере». Для того чтобы лететь к Луне космонавтам, вообще затевать пилотируемые полеты со скоростями порядка второй космической ~11 км/с и выше, нужна одна малость. Сущая безделица: возможность вернуться на Землю. И желательно живыми. При спусках даже с первой космической скоростью ~7,8 км/с и даже при минимальных углах входа, спуск симметричной неориентируемой капсулы сопровождается перегрузками до 9 g. И хотя они не являются смертельными, тем не менее, опасны для здоровья космонавтов, и по возможности желательно их избегать. Модель дана с учетом поправки влияния боковой силы на максимальную перегрузку, которую испытывают астронавты. Так как у читателей могут возникнуть вопросы, я решил проиллюстрировать вышесказанное графическими построениями численных расчетов при разных параметрах. Красным цветом показана траектория полета, синим значение текущей перегрузки в [м/с²].

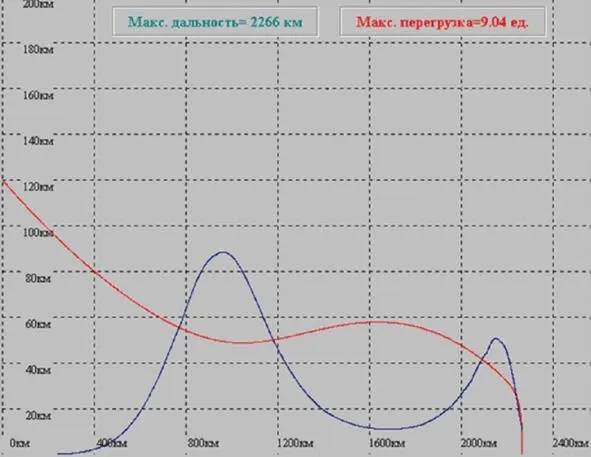
На графике показана траектория спуска капсулы при угле входа -6,5° и параметром управления по крену, исходя из расчетной дальности ~2260 км или ~1220 морских миль. Перегрузка достигла 9,04 g. При расчетной дальности более 9000 км перегрузка не более 4,86 g. Такой профиль траектории соответствовал спуску СА «Зонд». Когда ставилась задача расчета спуска в атмосферу со второй космической скоростью, то выяснилось, что даже в случае попадания в очень узкий коридор шириной в 1° то и в таком случае перегрузки будут выше 10 g – на практике они, достигнут значений порядка 15 g ÷ 20 g. На графике показана траектория спуска капсулы при угле входа -5,9°(в коридоре -5,6°÷ -6,1°). Поэтому ученые умы придумали ход – спускаться не в одно «касание», а в два. При первом погружении капсула теряет скорость до величины порядка первой космической скорости.