Аркадий Велюров - Пепелацы летят на Луну. Большой космический обман США. Часть 10

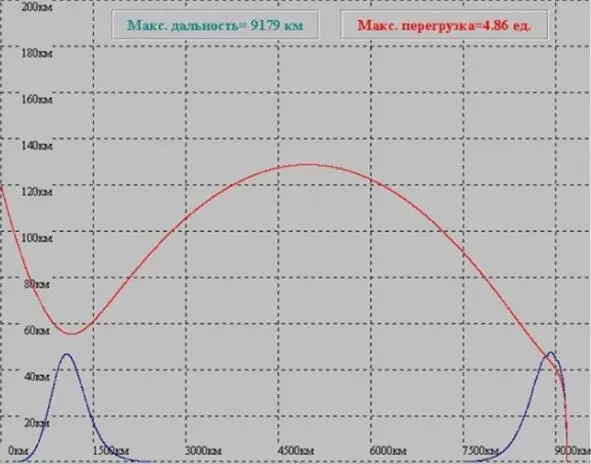
График №2. При втором погружении происходит штатный спуск, как при возвращении с орбиты спутника Земли. Максимальная перегрузка будет 4,86 единиц. Максимальная дальность 9179 км. Как говорят математики, эту задачу к предыдущей задаче. Не надо думать, что такая идея была достоянием только советских ученых. В документах НАСА имеется четкое указание, что в начале 60-х годов, они прорабатывали точно такую же схему. Она была показана выше на рисунке 2: «Двойное погружение в атмосфере» и рисунке 5. «Двойное погружение и прыжок, НАСА». Тем более странно и нелепо в последствие оказалось, что в отличие от двухнырковой схемы спуска советских «Зондов», американские «Аполлоны» после возвращения с Луны садились «тупо» – «в лоб» одним нырком и достаточно коротким участком приземления (~2250 км) между точкой входа и точкой приводнения. Напомню, что отличительной особенностью двухнырковой схемы является очень большой «тормозной» путь – порядка ~8000…10000 км. При чем, что особо интересно – корабль А-7 при возвращении с орбиты ИСЗ имел длину тормозного участка порядка ~3000 км. То есть больше, чем у всех Аполлонов, кроме А-9. Но и тот дальше орбиты ИСЗ не летал. Теперь давайте попробуем вооружиться двумя программами расчета спуска капсулы на Землю, и численно посчитать «эволюцию» спускаемого аппарата в плотных слоях атмосферы. Первая программа и модель принадлежит автору статьи, вторая (для сравнения и оценки) – взята здесь: «ReentryModel. zip». Для справки: «Reentry Model – модель объекта, возвращающегося в атмосферу; модель явления при возвращении в атмосферу». (Примечание речь идет о компьютерной программе).

Описание модели автора: Модель атмосферы была взята согласно справочного издания Министерства обороны СССР. Модель для численного счета описывается следующим образом (управление по дальности и боковому маневру реализовано через управление по каналу крена капсулы):

ρ=ρ (h) – плотность воздуха;

S – рабочая поверхность капсулы;

μ – гравитационный параметр Земли;

C x C у – аэродинамические коэффициенты осевой и нормальной силы;

Силы, записанные в соответствующем виде для скоростной системы координат:

Q=C x*S*ρ (h) *v²/2m – осевая сила сопротивления, приведенная на массу капсулы;

N=C y*S*ρ (h) *v²/2m – нормальная (подъемная) сила, приведенная на массу капсулы;

P у=N*cos (γ) – результирующая нормальная сила с учетом параметра управления по крену cos (γ)

Связь для субъективно ощущаемой перегрузкой такова:

n= (Q + P y + P z) /m – векторное равенство; при этом необходимо учесть, что боковая проекция нормальной силы

P z=N*sin (γ) хотя и не участвует в уравнениях движения в плоской модели (Х,У), но важна для целей определения максимальной перегрузки. Перегрузка в единицах [м/с 2] |a’|=|n|; или в относительных единицах

n=|a’|/g0; при этом ускорение ц.м. капсулы в координатах ХУ равно:

a= (Q + P y + W) /m; где сила тяжести W=mg;

Для прямоугольной системы координат Х,У (начало СК связано с центром Земли, ось У проведена через точку входа в атмосферу, ось Х перпендикулярна У и лежит в плоскости спуска капсулы) проекции на оси Х,У (здесь мы для простоты опускаем боковую проекцию Z и ведем расчет только в плоскости Х,У):

x″ = —Q* (v x/v) —P у* (v y/v) – (μ/r²) *x/r

y″ = —Q* (v y/v) +P у* (v x/v) – (μ/r²) *y/r

При этом учитываем следующую связь переменных:

x′ = v x y′ = v y; v² = v x² + v y²; r² = x² + y²

H = r – r 0

начальные условия: m/S = 465кг/м²; C x =0,85; C у /C х=0,34;

tg (α) = v y /v x —начальный угол; v = v 0; H = H 0;

управление (исходя из заданной дальности L) реализуется изменением угла крена – путем уменьшения

Су»=Су*cos (γ)

Дальность 2250 км достигнута при

К=Су»/Сх=0,136.

При численном решении системы уравнений использовался метод Адамса четвертого порядка вида:

J y = (55y’ i – 59y’ i-1 +37y’ i-2 – 9y’ i-3) /24

y i+1 = y i + J y*Δt

Шаг счета h=0,1сек. Погрешность решения, найденного многошаговым методом, оценивается как

|y i – y i* | 4).

Вторая модель расчета

Особенности программной реализации второй модели автору не известны. Однако анализируя данные, автору удалось установить, что на диаграмме «Асс» эта программа показывает непосредственно перегрузку, а не скажем общее ускорение капсулы. Работа с программой начинается с введения исходных данных. Все данные автор ввел аналогично собственной программе, за исключением параметра управления К. Вместо К=0,136 пришлось взять К=0,152 для достижения нужной дальности ~2250 км. Данные вносятся в формочку в таком виде:

Vehicle: m (kg) 5560; S (m2) 11,9;

Cx 0,85; K 0,152.

Initial conditions: H (km) 120;

V (m/s) 11030; a-6,5S;

imulation parameters Dt 1.

Constants: g (stand) 9,8068; g (polar) 9,8322;

Earth radius (km) 6378 m 4,0E+14;

Air density 1,29.

Landing Time (s) 9,02;

Range (km) 2251.

После внесения данных рядом с таблицей программа рисует диаграммы траектории, ускорения и скорости капсулы в каждой точке полета, а также текстовый транскрипт эволюции полета.

Обсуждение результатов расчета: Если принять угол входа в районе -6,5° то максимальные перегрузки, при управляемом спуске достигнут ~9 g, баллистический спуск ~16 g (примерно под таким углом входил «Зонд-5», так что данные численного расчета совпадают с данными конкретного полета). Для крайних случаев с максимальным углом входа -7,08°(«Аполлон-4») перегрузки составят ~12 g при управляемом спуске, и ~22 g на баллистике. На графике 1, указанном выше, показана траектория спуска капсулы. Красным цветом показана траектория полета, синим – значение текущей перегрузки в [м/с²]. С учетом угла входа -6,5° и параметров управления по крену, исходя из расчетной дальности ~2260 км.

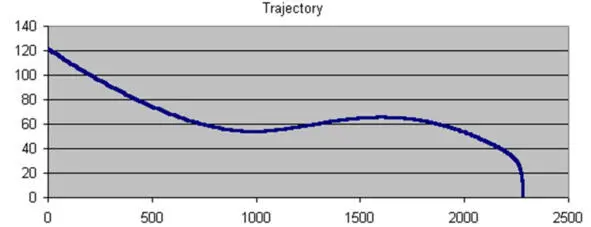
Как видите, максимальная перегрузка достигла 9,04 g.

А вот данные моделирования второй программой «асс».

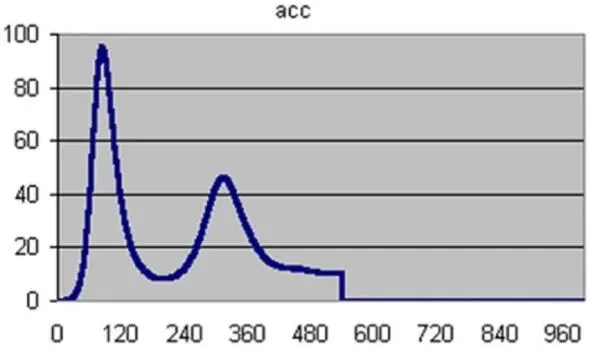
Согласно данных текстового транскрипта, на 81-й секунде отмечено прохождение максимума перегрузки а=99 м/с² или ~10 g при скорости 9 км/с на высоте 54,3 км.

На графике №2, выше, показана траектория спуска капсулы при угле входа -5,9°(в коридоре -5,6°÷ -6,1°). При расчетной дальности более 9000 км перегрузка не более 4,86 g. Такой профиль траектории соответствовал спуску СА «Зонд».

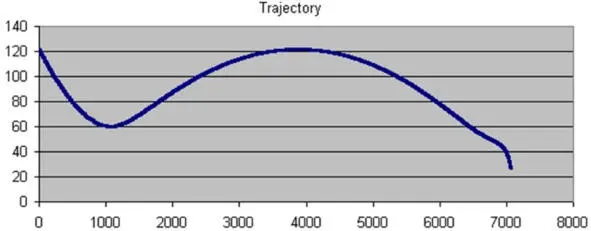
Для сравнения: в авторской программе максимум достигался на 91-й секунде при скорости 8,9 км/с на высоте ~50 км. Значение перегрузки ~89 м/с² или ~9 g.

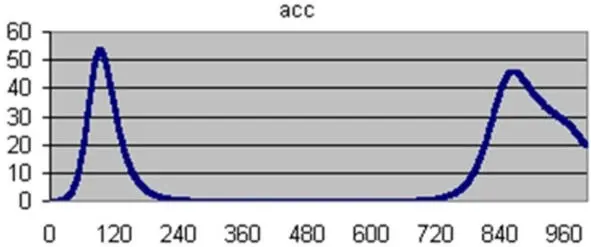
Численное моделирование на компьютере показывает, что при входе в секторе от -5,6° до -6,1° капсула Аполлона испытала бы максимальные перегрузки в пределах 4÷7 единиц с возможностью «прыжка» на расстояние 6000 км …9000 км. А в случае срыва на баллистический спуск перегрузки не превысят 10÷11 единиц. Вторая программа не позволяет делать расчеты траекторий спуска длиннее 7000 км. Поэтому был взят расчет семитысячного прыжка. Согласно данных текстового транскрипта, на 90-й секунде отмечено прохождение максимума перегрузки а=57,5 м/с² или ~5,8 g при скорости 9,7 км/с на высоте 59,7 км. Для сравнения: в авторской программе максимум достигался на 100-й секунде при скорости 9,7 км/с на высоте ~55,8 км. Значение перегрузки а=~47,6 м/с² или ~4,9 g. Имеется также второй максимум: а=48,3 м/с² или ~4,9 g на 1150-й секунде перед самой посадкой на высоте 43,2 км и скорости 4,3 км/с.