Вильгельм Оствальд - Искусство цвета. Цветоведение: теория цветового пространства

Общая форма фигуры, полученной таким путем, будет двойным конусом (рис. 15), получающимся от вращения равностороннего треугольника вокруг одной из его сторон, как вертикальной оси. Верхний конец двойного конуса содержит белый цвет, а нижний конец – черный. По экваториальной окружности расположены полные цвета. На поверхности верхнего конуса лежат все светло-чистые цвета, располагающиеся от полного цвета окружности к белой вершине конуса. Поверхность нижнего конуса содержит таким же образом темно-чистые цвета. Внутренность двойного конуса заключает в себе все тусклые цвета, при чем все светлотусклые цвета собраны в верхней половине конуса, а темные в нижней. Наиболее же чистые цвета расположены по окружности.

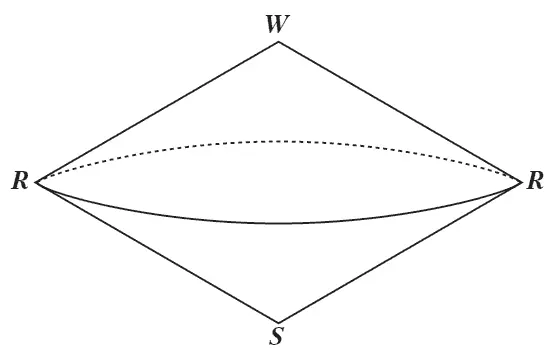
Рис. 15

В зависимости от того, какие мы берем треугольники, аналитические или логарифмические, мы и получаем аналитическое или логарифмическое цветовое тело. Для всех практических целей имеет значение исключительно логарифмическое цветовое тело. Для некоторых же теоретических вопросов предпочтительно бывает аналитическое. Мы должны поэтому ознакомиться и с тем, и с другим.

Логарифмическое цветовое тело так же, как и соответствующие ему треугольники, в своем нижнем конце не ограничено и имеет довольно неправильное очертание, зависящее от современных технических возможностей; сообразно с успехами техники, оно медленно растет вниз.

Вместо непрерывно, плавно вращающегося треугольника, который образует цветовое тело благодаря изменению цветного тона с каждым поворотом, у нормированного цветного тела мы имеем 24 различных и раздельных треугольника, соответствующие нормам цветовых тонов. Рис. 16 дает приблизительное представление об этом расположении; каждый треугольник содержит, если он заканчивается на ступени р, свои 28 однотонных хроматических полей.

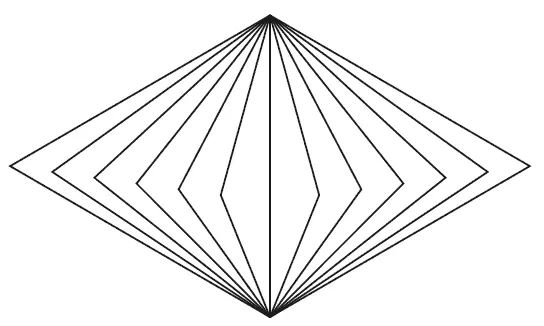
Рис. 16

При вращении равно-белых и равно-черных, они описывают соответствующие поверхности конусов, которые пересекают друг друга, разбивая все цветовое тело на 28 колец с ромбовидным сечением. Каждое из них составляет цветовой круг, так как содержит все 24 нормы цветовых тонов. Эти кольца пересекаются двадцатью четырьмя поверхностями однотонных треугольников, разбиваясь на двадцать четыре равных отрезка, каждый из которых соответствует одному из нормированных цветов. Если мы останавливаемся на ступени р, то число этих отрезков равно 28 × 24=672. Сюда нужно еще прибавить 8 ахроматических цветов, которые образуют среднюю колонку или ось.

Только что описанные кольца имеют для расположения цветов большое значение. Они содержат «равнозначные» цвета, т. е. такие цвета, которые обозначены одинаковыми буквами. Сумма этих цветов дает цветовой круг, а поэтому они представляют собой равнозначные цветовые круги. Относящиеся сюда цвета показывают какое-то особенно близкое сходство между собою. Это давно уже было замечено художниками, хотя и не было ими осознано. Они обозначали такие цвета, как цвета одинакового «Valör’a». Отсюда и произошло их название: «равнозначные», или «равноценные».

При этом удалось с большой пользой для дела и здесь заменить точным нормированием и точным определением все то, что раньше было неточно, недостоверно, и определялось лишь на глаз. Равнозначными цветами являются такие цвета, которые содержат одинаковые количества как белого, так и черного.

Таких равнозначных кругов в цветовом теле имеется 28, если мы ограничиваемся ступенью р. Они разного диаметра в зависимости от чистоты цвета. Все круги с чистотой цвета II находятся ближе всех к вертикальной оси. Вместе они образуют тонкий длинный цилиндр, состоящий из семи колец, что соответствует буквам са ес ge ig li nl рn. За ним идет следующий, более короткий, цилиндр с шестью кольцами еа gc ie lg ni pl. Следующий за ним состоит из 5 колец: ga ic le ng pi.

Затем следует цилиндр ia lc ne pg, за ним la nc ре, a за этим na pc, и, наконец, находится кольцо ра. Каждый равнозначный круг может поэтому обозначаться двумя буквами, которые указывают на одинаковое содержание белого и черного во всех принадлежащих ему 24 цветах. Вышеописанные цилиндры содержат цвета одинаковой чистоты, дающие ряды затененности (Schattenreihen). Можно, конечно, располагать кольца и по равно-белым и равно-черным цветам; в таком случае эти цвета будут иметь в своем обозначении одинаковой или первую, или вторую букву. Подобные кольца образуют поверхности, параллельные нижней или верхней поверхности двойного конуса. Соединения цветов по таким признакам имеют, однако, мало значения.

Равнозначные круги дают основание для создания цветовых гармоний из различных цветовых тонов, в то время как в однотонных треугольниках даны бывают гармонии одинаковых цветовых тонов. Мы еще вернемся в дальнейшем к рассмотрению равнозначных цветов.

Часто высказывалось и применялось следующее основное правило нормирования: точки норм должны равноотстоять друг от друга и нигде не быть слишком тесно расположенными, или же слишком редкими. При разделении шкалы серых цветов мы строго придерживались этого предписания, и можно было бы предполагать, что можно будет его придерживаться и в дальнейшем для всего цветового тела. Это, однако, не совсем так. Ведь отрезки равнозначного круга тем больше или меньше, чем больше или меньше их чистота. В наименее чистых кругах са ес и т. д., которые суть круги самые маленькие, все двадцать четыре цветовых тона более тесно лежат друг к другу, чем в последующих кругах, и эти расстояния увеличиваются по мере увеличения чистоты цветов.

Это сказывается также и при изготовлении кругов. В то время как цвета круга ра установить с точностью до одной точки деления на сто и где можно определить даже дробные части, совершенно не представляет никаких трудностей, круг чистоты II, и особенно более темные, вызывают большие затруднения, и только с большим трудом удается приготовить их с точностью до одной ступени.

Это есть безусловно несовершенство с точки зрения нормирования, а посему и не было недостатка в предложениях уменьшить в менее чистых кругах число цветовых тонов до 12, 8, 6 и даже 4, для того, чтобы повсюду иметь приблизительно одинаковые различия. Все-таки недостатки такого нормирования оказались настолько большими, что от него пришлось отказаться.

Причина та, что только лишь тем путем, который был описан раньше, можно получить 24 полных однотонных треугольника, которые нужны не только для логичности построения цветового тела, но и практически для нахождения гармоний равных цветовых тонов. В ином же случае мы получили бы только четыре полных треугольника, другие же обрывались бы, не достигая серой оси. Это особенно выделяло бы четыре цветовых тона в ущерб другим тонам, без того, чтоб такое выделение было достаточно обосновано. Лучше уж согласиться с недостатками таких рядов вблизи серой оси (как, напр., у темных цветов чистоты II); ряды IV приготовляются уже полностью без большого труда. Наш случай вполне аналогичен с делением на градусы земного шара, где круги меридианов также все ближе сближаются у полюсов. Все-таки это общепринятое деление имеет в остальном настолько большие преимущества, что указанным недостатком можно пренебречь. То же самое верно и по отношению к нормированию цветового тела. Откажись мы от построения полных однотонных треугольников, – возможности выбора цветовых гармоний особенно бы от этого пострадали.