Дэвид Уоллес - Бесконечная шутка

118. …еще как-то пропущено, что Марио гомодонт: все его зубы – идентичные премоляры, и передние, и задние, как у морской свиньи; это источник бесконечных терзаний для Теда Шахта, который избегает Марио, если тот рядом, потому что борется с желанием попросить сказать «А» и подвергнуть рот изучению, что, как хорошо представляет Шахт, наверняка ранит чувства Марио: кому же хочется ни с того ни с сего почувствовать себя клинической диковинкой.

119. Феномен, который уже способные к абстрактному мышлению постгегельянские взрослые зовут «историческим сознанием».

120. Преди постпроцедуры Эсхатона такие запутанные, что до игры дело доходит только где-то раз в месяц, не чаще, и почти всегда по воскресеньям, но и тогда не у всех двенадцати детей есть время на игру, вот почему количество участников указывается с таким запасом.

121. Онанская картографическая серия для школ, W–520–500–268–6W– 9W–9W–14W4 ©1994 до э. с., «Рэнд Макнэлли и Ко».

122. Это Пемулис, диктую Инку, который пусть и дальше сидит, многозначительно складывает пальцы домиком, прижимает к губам и ничего не записывает, а потом, типа, накатает все это в любое время на следующей неделе дословесно (sic), засранец наглый. Итак, теорема конечных приращений для дележа общего мегатоннажа среди Комбатантов, чьи соотношения ВНП / Военный бюджет // ВБ / Расходы на ядерку варьируются от Эсхатона к Эсхатону, спасет вас от высчитывания соотношений каждый раз для каждого Комбатанта, потом прокатить результат через множественную регрессию, чтобы Комбатанты вознаграждались за то, что не скупились на термояд в прошлый раз (вербальные украшательства авторства Хэла. – ХДИ). Эту теорему также можно доказать с помощью теоремы Вейерштрасса, у которой самой доказательство – самая здоровая мозговыносящая хреновина с морковиной во всем дифференцировании, но вот уже вижу, как Хэла перекосило, так что давайте по-быстрому, хотя, короче, все это реально интересно, если вам интересно, и все такое.

Вот, скажем, дано: Комбатант и его прошлые соотношения ВНП/ВБ // ВБ/ РЯ. Найти: точное среднее число всех прошлых мегатоннажей, которые были у Комбатанта в прошлом. Точное среднее число и называется «конечное приращение», над чем можно пока похихикать, раз у нас тут контекст конца света и все такое.

И ну пока суть (sic) да дело, короче, пусть А – конечное приращение постоянно флуктуирующего соотношения Комбатанта и такого же постоянно флуктуирующего изначального мегатоннажа. Надо найти А и выдать Комбатанту на руки ровно А мегатонн. Делается это чертовски элегантно, и все, что вам для этого понадобится, – два параметра: самое большое его соотношение за историю игры и самое маленькое. Эти две цифири называются экстремальными значениями функции cn-n, у которой-то А и есть, кстати говоря, конечное приращение.

И ну так вот, но тогда пусть / будет непрерывной неотрицательной функцией (то бишь соотношением) на интервале [a, b] (то бишь разница между самым меньшим соотношением и самым большим и все такое). Что, мои лирические отступления раздражают? Инк на меня тут так смотрит, что кровь в жилах стынет. Ну, трудно понять, что разжевывать, а что и так все знают. Я пытаюсь рассказать все самым максимально (sic) понятным способом. А теперь он смотрит так, будто я отвлекаюсь. Инкулятор, ты просто возьми из моих объяснений только нужных вещей (sic), а остальное не записывай. Но так, да, у нас есть / и у нас есть [a, b]. И пусть г и R будут минимальным и максимальным значением функции /(x) на интервале [a, b]. И ну теперь заценим прямоугольники высоты г и R на интервале [a, b] на графике под названием – а ну давайте назовем его ПЕМСТЕР:

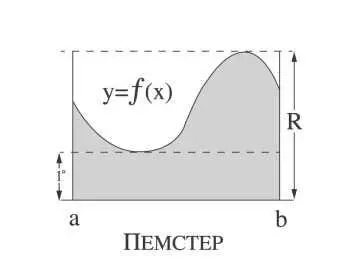
Конечное приращение, которое мы ищем, А, теперь можно выразить интегрально как площадь какого-то среднего прямоугольника, высота которого вышее (sic), чем г, но корочее (sic), чем R. Остается самая легкотня. Нужна константа. Без константы по жизни никуда. Теперь Инк саркастично кивает, будто я завернул афоризм. Пусть d будет константой – и по причинам легкости расчетов чем ближе к 1, тем лучше, так что положим d размером с Блок Хэла.

Примечание Хэла Инканденцы: В метрах.

Возвращение Майкла Пемулиса: Оборжаться. И ну короче, просто глядя на охренительно просветительный (sic) график ПЕМСТЕР выше, сразу понятно, что площадь, которую мы ищем:

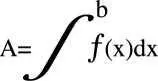
а

)м меньше пло-

будет больше площа/

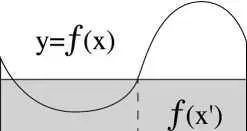
щади прямоугольника с высотой R. Вследствие (sic), чистый здравый разум (sic) говорит нам, что где-то между r и R есть такая высота f (x), что (надо, кстати, заметить, что в каждом доказательстве теоремы есть «пусть», «положим» и «такая, что» – по-моему, в основном потому, что это пафосно звучит), такая, что прямоугольник с этой высотой f (x) на всем интервале [a, b] имеет именно ту площадь, что мы ищем, – конечное приращение всех историчных (sic) соотношений расходов; нашими деньгами, в абстрактной форме

f (x)dx = f (x')(b – a)

b

a

x'

ХРЕНХЭЛА

Работает, епта. И не надо каждый раз высчитывать соотношения для каждого Комбатанта, чтобы раздать арсенал. Просто берешь высшие и низшие соотношения из записей Эсхатонов, которые Шапка ведет каждую игру, и все. Лепота. Элегантно, епта. Отметьте, что («отметьте, что» – еще один, типа, своеобыч-

где (b – a) – размер интервала. И ну и теперь обратимся к срывающему покровы графику под названием ХРЕНХЭЛА:

ный (sic) термин), отметьте, что мегатоннаж Комбатантов будет меняться, слегка, от Эсхатона к Эсхатону, точно так же, как средний показатель подающего немного меняется от выхода на биту к выходу на биту, в интегральной зависимости от того, что он выдал в последний выход на базу и все такое. Также отметьте, что волшебную формулу конечных приращений можно применять ко всему, что варьируется в (определяемых) рамках и все такое – типа, любая линия, или границы теннисного корта, или, типа, например, скажем, диапазон уровня чистоты мочи для любого наркотика между «Все чисто» и «Песец». В качестве типа упражнения, если интересно, поиграйте три часа в топовый юниорский теннис высокого уровня (sic), а потом рассчитайте конечное приращение соотношений первых подач к выходу к сетке и выходов к сетке к отыгранным очкам; для сеточника это лучший способ понять, как сильно зависит его игра от подачи. Делинт щелкает такие задачки каждое утро, не слезая с толчка. А теперь даже интересно, как Инк – который мнит, что слишком хорош, чтобы расписать Эсхатон от третьего склонения (sic), как какой-нибудь высухопарный (sic) эсхатолог с кожаными заплатками на локтях (sic), – как вот Инк транспонирует (sic?) всю мою математику без помощи своей мамуси. Покеда.