БСЭ - Большая Советская энциклопедия (Но)

Вдоль главной диагонали расположены специальные квадратные клетки (на схеме они обведены пунктиром). Все элементы матрицы, расположенные вне этих клеток, равны нулю. В каждой диагональной клетке вдоль главной диагонали повторяется одно и то же (комплексное) число (в первой клетке l 1, во второй l 2и т. д.); параллельный ряд над главной диагональю состоит из единиц. Все же остальные элементы в диагональных клетках равны нулю. На приведённой схеме имеются три диагональные клетки, из которых первая имеет порядок 4, вторая и третья — порядок 2. В общем же случае число клеток и порядки их могут быть любыми. Среди чисел l 1, l 2…. возможны и равные. Исходная матрица А в указанном примере имеет следующие элементарные делители : (l — l 1) 4, (l — l 2) 2, (l — l 3) 2. По элементарным делителям матрицы однозначно определяется её жорданова форма.

Если матрица А имеет жорданову форму I , то существует неособенная матрица Т такая, что А = TIT -1. Замену матрицы А подобной ей матрицей I называют приведением матрицы А к нормальной жордановой форме.

Представление о применениях жордановой формы матрицы можно получить на примере системы линейных дифференциальных уравнений с постоянными коэффициентами:

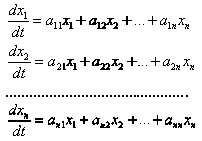
в матричной записи:

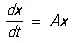
Введём новые неизвестные функции y 1, у 2…. y nпри помощи неособенной матрицы 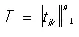[ t ik— числа ( i, k = 1, 2, …, n)]:

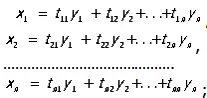
в матричной записи:

х = Ту .

Подставляя это выражение для x в (2), получим:

где матрица I связана с матрицей А равенством:

А = TIT -1.

Обычно матрицу Т подбирают так, чтобы матрица А имела жорданову форму. В этом случае система уравнений (3) значительно проще системы (2). Так, например, при n = 8, если матрица 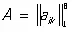имеет жорданову форму (1), то система (3) будет иметь вид:

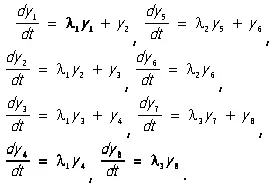
Интегрирование такой системы сводится к многократному интегрированию одного дифференциального уравнения.

Лит . см. при ст. Матрица .

Норм альная пл оскостьпространственной кривой в данной её точке М — плоскость, проходящая через М перпендикулярно к касательной прямой в той же точке. Н. п. содержит все нормали к кривой, проходящие через данную точку. Если кривая задана в прямоугольных координатах уравнениями х = f ( t ), у = g ( t ), z = h ( t ), то уравнение Н. п. в точке М ( х 0, у 0, z 0), соответствующей значению t 0параметра t , может быть написано в виде:

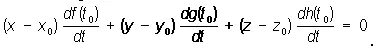
Норм альная произв одная, производная, взятая от функции, заданной в пространстве (или на плоскости), по нормали к некоторой поверхности (соответственно, линии, лежащей в той же плоскости). Пусть S — поверхность, Р — точка поверхности S , а функция f задана в некоторой окрестности точки Р . Тогда Н. п. от f в точке Р равна пределу отношения разности f ( A ) — f ( P ) (где А — точка нормали к поверхности S в точке Р , стремящаяся к Р с одной стороны S ) к расстоянию от A до Р (см . рис. ). Смотря потому, с какой стороны А приближается к Р , различают производную от f по внешней и по внутренней нормали к S . Рассмотрение Н. п. особенно важно в теории краевых задач .

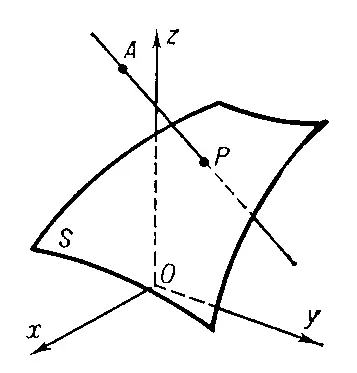
Рис. к ст. Нормальная производная.

Норм альное распредел ение, одно из важнейших распределений вероятностей. Термин «Н. р.» применяют как по отношению к распределениям вероятностей случайных величин, так и по отношению к совместным распределениям вероятностей нескольких случайных величин (т. е. к распредслениям случайных векторов).

Распределение вероятностей случайной величины Х называется нормальным, если оно имеет плотность вероятности . (*)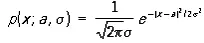

Семейство Н. р. (*) зависит, т. о., от двух параметров а и s. При этом математическое ожиданиеХ равно а, дисперсияХ равна s 2. Кривая Н. р. у = р ( х;а , s) симметрична относительно ординаты, проходящей через точку х = а , и имеет в этой точке единственный максимум, равный 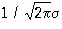. С уменьшением s кривая Н. р. становится всё более и более островершинной (см . рис. ). Изменение а при постоянном s не меняет форму кривой, а вызывает лишь её смещение по оси абсцисс. Площадь, заключённая под кривой Н. р., всегда равна единице. При a = 0, s = 1 соответствующая функция распределения равна

.

В общем случае функция распределения Н. р. (*) F ( х;а , s) может быть вычислена по формуле F ( x;а , s) = Ф ( t ), где t = ( х — а )/s. Для функции Ф ( t ) (и нескольких её производных) составлены обширные таблицы. Для Н. р. вероятность неравенства 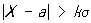, равная 1— Ф ( k )+ Ф (— k ), убывает весьма быстро с ростом k (см. таблицу).

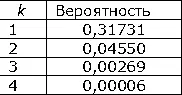
Во многих практических вопросах при рассмотрении Н. р. пренебрегают поэтому возможностью отклонений от а , превышающих 3s, — т. н. правило трёх сигма (соответствующая вероятность, как видно из таблицы, меньше 0,003). Вероятное отклонение для Н. р. равно 0,67449s.

Н. р. встречается в большом числе приложений. Издавна известны попытки объяснения этого обстоятельства. Теоретическое обоснование исключительной роли Н. р. дают предельные теоремы теории вероятностей (см. также Лапласа теорема, Ляпунова теорема ). Качественно соответствующий результат может быть объяснён следующим образом: Н. р. служит хорошим приближением каждый раз, когда рассматриваемая случайная величина представляет собой сумму большого числа независимых случайных величин, максимальная из которых мала по сравнению со всей суммой.