БСЭ - Большая Советская энциклопедия (Но)

Физическое значение Н. в. определяется тем, что в области, свободной от источников, любое возмущение может быть представлено в виде суперпозиции Н. в., причём результирующий поток энергии (упругой или электромагнитной) равен сумме потоков во всех Н. в. В этом отношении понятие Н. в. в волновой теории играет роль, аналогичную понятию нормальных колебаний в теории колебательных систем.

Вдоль границы раздела двух сред могут распространяться поверхностные Н. в., например рэлеевские волны на границе упругого тела ( рис. 2 ), т. н. медленные электромагнитные волны в замедляющих структурах и др. В случае Н. в. в многопроводных связанных линиях передачи, используемых в технике связи, в направлении распространения сохраняется не поперечное распределение поля, а отношение амплитуд колебаний на отдельных проводах.

Наконец, Н. в. в безграничных и однородных сплошных средах — это плоские волны , сохраняющие при распространении свою поляризацию. Н. в. являются, например, обыкновенная и необыкновенная волны в одноосных кристаллах. Эти волны линейно поляризованы во взаимно перпендикулярных направлениях, причём поляризация этих волн сохраняется в направлении распространения ( рис. 3 ), в то время как поляризация произвольно поляризованной волны меняется от точки к точке. Др. примерами Н. в. в сплошных средах являются плоские упругие волны, эллиптически поляризованные электромагнитные волны в магнитоактивной плазме, циркулярно поляризованные волны в оптически активных средах.

Лит.: Горелик Г. С., Колебания и волны, 2 изд., М., 1959; Бриллюэн Л. и Пароди М., Распространение волн в периодических структурах, пер. с франц., М., 1959; Бреховских Л. М., Волны в слоистых средах, М., 1973; Вайнштейн Л. А., Электромагнитные волны, М., 1957; Бергман Л., Ультразвук и его применение в науке и технике, пер. с нем., М., 1956; Викторов И. А., Физические основы применения ультразвуковых волн Рэлея и Лэмба в технике, М., 1966.

Ю. А. Кравцов.

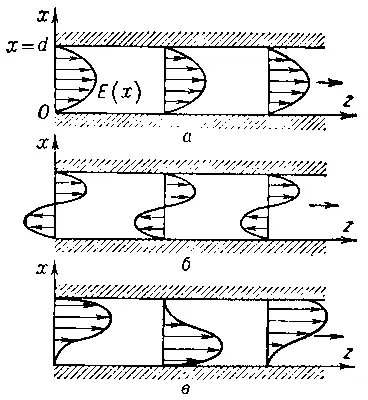
Рис. 1. Схема распространения двух нормальных волн а и б и волны в, полученной в результате их наложения. В сечениях 1 и 3 разность фаз нормальных волн φ = 0 и они складываются, а в сечении 2 φ = —π и волна вычитается.

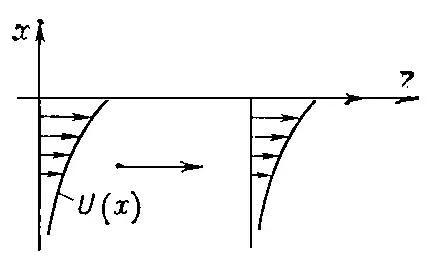
Рис. 2. Схема распространения рэлеевской волны на границе упругого тела.

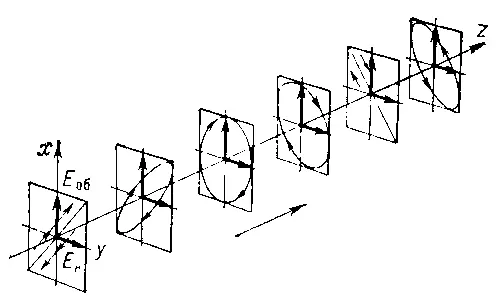
Рис. 3. Схема распространения обыкновенной и необыкновенной волн в одноосных кристаллах.

Норм альные колеб ания, гармонические собственные колебания , которые могли бы существовать в линейных колебательных системах, если бы в них не происходило рассеяния энергии. В каждом Н. к. все точки системы колеблются с одной и той же частотой, которая (так же, как и распределение амплитуд и фаз Н. к. между точками системы) определяется параметрами системы. Число Н. к., свойственных данной колебательной системе, равно числу колебательных степеней свободы (см. Степеней свободы число ) в этой системе; в частности, сплошной колебательной системе, число степеней свободы которой n = ¥, свойственно бесконечно большое число Н. к. (при этом частоты всех Н. к., вообще говоря, различны, и только в специальных «вырожденных» случаях частоты некоторых Н. к. могут быть равны).

Все Н. к. независимы в том смысле, что специальным выбором начальных условий можно возбудить только одно (любое) из всех свойственных системе Н. к. Но при произвольных начальных условиях в общем случае возбуждаются одновременно все n Н. к., и в каждом из этих колебаний участвуют все n колебательных степеней свободы. Результирующее колебание, представляющее собой сумму всех возникших Н. к., уже не является гармоническим. Величины амплитуд и начальных фаз всех Н. к. определяются начальными условиями.

Любое, т. е. возникающее при любых начальных условиях, негармоническое собственное колебание в линейной системе представляет собой суперпозицию свойственных этой системе Н. к. В то же время резонанс в колебательной системе может возникнуть лишь в том случае, когда частота гармонической внешней силы совпадает с одной из частот Н. к. в этой системе. Т. о., состав Н. к., свойственных данной системе, существенно определяет черты как собственных, так и вынужденных колебаний в данной системе. Число колебательных степеней свободы, а значит, и число Н. к., свойственных системе, равно или меньше общего числа степеней свободы этой системы.

Лит.: Горелик Г. С., Колебания и волны, 2 изд., М., 1959, гл. VI, § 9; Стретт Дж. В. (лорд Рэлей), Теория звука, пер. с англ., 2 изд., М. — Л., 1955, гл. VI, § 86.

С. Э. Хайкин.

Норм альные уравн ения, некоторая специальная система алгебраических или трансцендентных уравнений, решение которой даёт приближённые значения неизвестных величин, оцениваемых способом наименьших квадратов. См. Наименьших квадратов метод .

Норм альные усл овия, 1) условия применения средств измерений, при которых влияющие величины (температура, питающее напряжение и др.) имеют нормальные (установленные) значения или находятся в пределах области допускаемых отклонений от этих значений. Н. у. указываются на шкалах средств измерений, в стандартах на них, технических описаниях и инструкциях к использованию. Пределы допускаемых основных погрешностей средств измерений устанавливаются для Н. у. Для электроизмерительных приборов за Н. у. часто принимают следующие: температура — в пределах 20 ± 2 °C, питающее напряжение — указанное на шкале ± 2 %, частота — в пределах 49–51 гц и т. д. 2) Физические условия, определяемые давлением р = 101325 н/м 2= 760 мм рт. ст . (нормальная атмосфера) и температурой 273,15 К (0 °C), при которых мольный объём идеального газа V o= 2,24136 · 10 -2 м 3/ моль . Нормальное ускорение свободного падения принимают равным g n = 9,80665 м/сек 2.

К. П. Широков.

Норм альные шк олы, педагогические учебные заведения, обычно готовящие учителей для начальных школ. Возникли в Австрии во 2-й половине 18 в., во Франции в конце 18 в.; получили распространение в англо-саксонских странах в 19 в., где позднее стали называться учительскими или педагогическими колледжами. Н. ш. существуют во Франции, Бельгии, Люксембурге, французских районах Швейцарии и Канады, во многих странах Латинской Америки и в некоторых африканских странах.