БСЭ - Большая Советская энциклопедия (Но)

Н. р. может появляться также как точное решение некоторых задач (в рамках принятой математической модели явления). Так обстоит дело в теории случайных процессов (в одной из основных моделей броуновского движения ). Классические примеры возникновения Н. р. как точного принадлежат К. Гауссу (закон распределения ошибок наблюдения) и Дж. Максвеллу (закон распределения скоростей молекул).

Совместное распределение нескольких случайных величин X 1, X 2…., X sназывается нормальным (многомерным нормальным), если соответствующая плотность вероятности имеет вид:

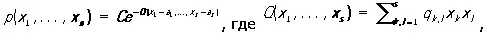
q k, l = q l, k — положительно определенная квадратичная форма. Постоянная С определяется из того условия, что интеграл от р по всему пространству равен 1. Параметры a 1 …., a s равны математическим ожиданиям X 1 …., X s соответственно, а коэффициент q k, l могут быть выражены через дисперсии s 1 2…., s s 2этих величин и коэффициент корреляции s k, l между X k и X l . Общее количество параметров, задающих Н. р., равно

( s + 1)( s + 2)/2 — 1

и быстро растет с ростом s (оно равно 2 при s = 1, 20 при s = 5 и 65 при s = 10). Многомерное Н. р. служит основной моделью статистического анализа многомерного . Оно используется также в теории случайных процессов (где рассматривают также Н. р. в бесконечномерных пространствах).

О вопросах, связанных с оценкой параметров Н. р. по результатам наблюдений, см. статьи Малые выборки и Несмещенная оценка . О проверке гипотезы нормальности см. Непараметрические методы (в математической статистике).

Лит . см. при ст. Распределения .

Ю. В. Прохоров.

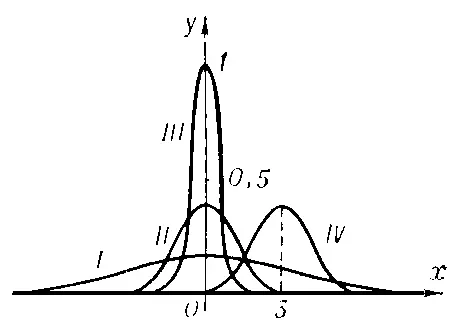
Кривые плотности нормального распределения для различных значений параметров а и s: I. а = 0, s = 2,5; II. a = 0, s = 1; III. a = 0, s = 0,4; IV. a = 3, s = 1.

Норм альное сеч ениеповерхности S в данной её точке М — линия пересечения S с плоскостью, проведённой через нормаль в точке М . С помощью Н. с. изучается искривление поверхности S в различных (касательных) направлениях, выходящих из точки М . Среди этих направлений имеются два (взаимно перпендикулярных) т. н. главных направления, для которых нормальная кривизна (т. е. кривизна соответствующего Н. с.) достигает наибольшего и наименьшего значений k 1и k 2(т. н. главные кривизны в данной точке); при этом кривизны Н. с. берутся со знаком + (или —), если направление вогнутости (см. Выпуклость и вогнутость ) сечения совпадает (противоположно) с положительным направлением нормали к поверхности. Нормальные кривизны поверхности в произвольных направлениях весьма просто выражаются через главные кривизны. Именно, кривизна k n Н. с., проведённого в направлении, составляющем угол j с первым из указанных выше главных направлений, связана с k 1и k 2соотношением (формула Эйлера):

k n = k 1cos 2φ + k 2sin 2φ.

С помощью кривизн Н. с. изучаются также кривизны наклонных сечений поверхности. Именно, кривизна k наклонного сечения плоскостью a, проходящей через данную касательную прямую а , выражается формулой Менье:

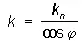
где φ — угол между плоскостью a и нормалью к поверхности, k n— нормальная кривизна поверхности в направлении прямой а . См. также Дифференциальная геометрия, Поверхностей теория, Кривизна .

Норм альное ускор ение, составляющая ускорения точки при криволинейном движении, направленная по главной нормали к траектории в сторону центра кривизны; Н. у. называется также центростремительным ускорением. Численно Н. у. равно v 2/r, где v — скорость точки, r — радиус кривизны траектории. При движении по окружности Н. у. может вычисляться по формуле r w 2, где r — радиус окружности, w— угловая скорость вращения этого радиуса. В случае прямолинейного движения Н. у. равно нулю.

Норм альностьв химии, концентрация раствора, выраженная числом грамм-эквивалентов растворённого вещества, содержащегося в 1 л раствора. Способ выражения концентрации растворов через Н. широко используется в аналитической химии. См. также Грамм-эквивалент и Концентрация .

Норм альные в олны, собственные волны, гармонические волны той или иной физической природы (электромагнитные, упругие и др.), сохраняющие при своём прямолинейном распространении поперечную структуру поля и (или) поляризацию. Этим Н. в. отличаются от всех других волн, способных распространяться в данной системе. Например, при распространении между параллельными металлическими плоскостями ( рис. 1 ) электромагнитных Н. в. поперечная (по отношению к направлению распространения) структура электрического поля Н. в. одинакова во всех сечениях. Поперечная же структура любых других волн, отличных от Н. в., при распространении не сохраняется. Так, форма волны, полученной в результате наложения двух Н. в., изображенных на рис. 1 , а и б, меняется от сечения к сечению ( рис. 1 , в).

Наибольший практический интерес представляют электромагнитные Н. в. в волноводных системах, используемых для передачи сообщений или электромагнитной энергии. К ним относятся радиоволноводы СВЧ, коаксиальные кабели, плазменные волноводы, ионосферные и тропосферные каналы дальней радиосвязи, световоды, выполненные в виде стеклянных волокон, т. н. квазиоптические линии передачи волн миллиметрового и субмиллиметрового диапазонов и т. д.

Важные применения находят Н. в. в акустических волноводных системах (акустические трубы, звуковые каналы в океане и тропосфере), упругие Н. в. — в пластинах (волны Лэмба, т. н. поперечные Н. в.) и стержнях (продольные, изгибные и крутильные Н. в.). Упругие Н. в. применяются, в частности, для создания ультразвуковых линий задержки и для определения упругих и др. параметров твёрдых тел.

Число Н. в. N , способных распространяться в перечисленных выше системах, зависит от соотношения между длиной волны l и поперечными размерами системы d . Для волн с фиксированной частотой это число всегда конечно, при этом чем больше отношение d /l, тем больше N . На очень низких частотах (т. е. при d /l << 1/2) может распространяться только одна Н. в. определённого типа, а в некоторых системах, например в полых радиоволноводах, распространение низкочастотных Н. в. вообще невозможно. Фазовые и групповые скорости Н. в. разных типов отличаются друг от друга (этим, в частности, объясняется искажение поперечной структуры поля при наложении нескольких Н. в., рис. 1 ). Поэтому для передачи информации желательно использовать только один тип Н. в.