БСЭ - Большая Советская энциклопедия (Пр)

Выяснение распределения П. ч. в натуральном ряде чисел является весьма трудной задачей чисел теории . Она ставится как изучение асимптотического поведения функции p( х ), обозначающей число П. ч., не превосходящих положительного числа х. Первые результаты в этом направлении принадлежат П. Л. Чебышеву , который в 1850 доказал, что имеются такие две такие постоянные а и А, что < p( x ) < при любых x ³ 2 [т. е., что p( х ) растет, как функция 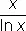]. Хронологически следующим значительным результатом, уточняющим теорему Чебышева, является т. н. асимптотический закон распределения П. ч. (Ж. Адамар , 1896, Ш. Ла Валле Пуссен , 1896), заключающийся в том, что предел отношения p( х ) к 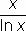равен 1.

В дальнейшем значительные усилия математиков направлялись на уточнение асимптотического закона распределения П. ч. Вопросы распределения П. ч. изучаются и элементарными методами, и методами математического анализа. Особенно плодотворным является метод, основанный на использовании тождества

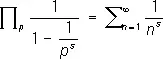
(произведение распространяется на все П. ч. р = 2, 3,...), впервые указанного Л. Эйлером ; это тождество справедливо при всех комплексных s с вещественной частью, большей единицы. На основании этого тождества вопросы распределения П. ч. приводятся к изучению специальной функции — дзета-функции x( s ), определяемой при Res > 1 рядом

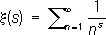
Эта функция использовалась в вопросах распределения П. ч. при вещественных s Чебышевым; Б. Риман указал на важность изучения x( s ) при комплексных значениях s . Риман высказал гипотезу о том, что все корни уравнения x( s ) = 0, лежащие в правой полуплоскости, имеют вещественную часть, равную 1/ 2. Эта гипотеза до настоящего времени (1975) не доказана; её доказательство дало бы весьма много в решении вопроса о распределении П. ч. Вопросы распределения П. ч. тесно связаны с Гольдбаха проблемой , с не решенной ещё проблемой «близнецов» и другими проблемами аналитической теории чисел. Проблема «близнецов» состоит в том, чтобы узнать, конечно или бесконечно число П. ч., разнящихся на 2 (таких, например, как 11 и 13). Таблицы П. ч., лежащих в пределах первых 11 млн. натуральных чисел, показывают наличие весьма больших «близнецов» (например, 10006427 и 10006429), однако это не является доказательством бесконечности их числа. За пределами составленных таблиц известны отдельные П. ч., допускающие простое арифметическое выражение [например, установлено (1965), что 2 11213—1 есть П. ч.; в нём 3376 цифр].

Лит.: Виноградов И. М., Основы теории чисел, 8 изд., М., 1972; Хассе Г., Лекции по теории чисел, пер. с нем., М., 1953; Ингам А. Е., Распределение простых чисел, пер. с англ., М. — Л., 1936; Прахар К., Распределение простых чисел, пер. с нем., М., 1967; Трост Э., Простые числа, пер, с нем., М., 1959.

Просто'й произво'дственный,временная приостановка работы по вине работника или по не зависящим от него причинам (поломка станка, отсутствие сырья, материалов, электроэнергии и т.д.).

В СССР за время П. п. не по вине рабочего или служащего заработная плата выплачивается в размере 1/ 2тарифной ставки повременной оплаты труда работника соответствующей квалификации, а в металлургической, горнорудной и коксовой промышленности — в размере 2/ 3тарифной ставки (месячная заработная плата в этих случаях не может быть ниже установленного минимального размера). На период освоения новых производств П. п. не по вине работника (как на новых, так и на действующих предприятиях) оплачивается из расчёта тарифной ставки повременщика соответствующего разряда. В тех отраслях народного хозяйства, где для рабочих-сдельщиков и рабочих-повременщиков установлены единые тарифные ставки, размер оплаты за время П. и. не по вине работника определяется законодательством СССР. Время П. п. по вине работника оплате не подлежит.

В случае П. п. рабочие и служащие переводятся (с учётом их специальности и квалификации) на другую работу на том же предприятии (в учреждении) на всё время П. п. либо на др. предприятие в той же местности на срок до 1 месяца. При переводе на нижеоплачиваемую работу вследствие П. п. за рабочими и служащими, выполняющими нормы выработки, сохраняется средний заработок по прежней работе, а за работниками, не выполняющими нормы или переведёнными на повременно оплачиваемую работу, сохраняется их тарифная ставка (оклад). Не допускается перевод квалифицированных рабочих и служащих на неквалифицированные работы.

Просто'й труд, труд работника, не имеющего квалификации , т. е. неквалифицированный труд. Всякий сложный труд может быть сведён к П. т., поскольку, по характеристике К. Маркса, «сравнительно сложный труд означает только возведенный в степень или, скорее, помноженный простой труд, так что меньшее количество сложного труда равняется большему количеству простого» (Маркс К. и Энгельс Ф., Соч., 2 изд., т. 23, с. 53). Редукция (сведение) сложного труда к простому (см. Редукция труда ) позволяет определить стоимость товаров. В рабочем часе сложного труда заключено несколько часов П. т., поэтому квалифицированная рабочая сила (см. Квалифицированный труд ) создаёт в единицу времени большую стоимость, чем рабочая сила без квалификации.

При капитализме сведение сложного труда к П. т. совершается стихийно, путём приравнивания (в процессе обмена) стоимостей товаров, созданных этими видами труда. В условиях социалистического общества происходит планомерное соизмерение затрат сложного труда и П. т. В процессе производства товаров сведение сложного труда к простому осуществляется на основе действия закона стоимости (см. Стоимости закон ).

В. В. Мотылёв.

Простоква'ша,см. Молочнокислые продукты .

«Просто'р»,литературно-художественный и общественно-политический иллюстрированный ежемесячный журнал. Орган СП Казахстана. Издаётся на русском языке в Алма-Ате с 1933 (до 1960 — под др. названиями). Журнал публикует художественные произведения, публицистику и очерки, критику, мемуары, материалы из литературного наследства. Тираж (1975) свыше 35 тыс. экз.

Лит.: Фоменко Л., Есть в Казахстане журнал..., «Литературная Россия», 1964, 23 окт.; Кузнецов П., Творческий поиск, «Правда», 1965, 25 апр.