БСЭ - Большая Советская энциклопедия (АН)

Интеграл от функции f = j + iy вдоль (ориентированной спрямляемой) кривой Г можно определить с помощью понятия криволинейного интеграла:

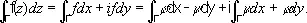
Центральное место в теории моногенных функций (теории Коши) занимает следующая итегральная теорема Коши: если функция моногенна в односвязной области D, то S Г f ( z ) dz = 0 для любой замкнутой кривой Г, лежащей в этой области. В произвольной области D то же утверждение справедливо для замкнутых кривых Г, которые непрерывной деформацией могут быть стянуты в точку (оставаясь в пределах области D ) . Опираясь на интегральную теорему Коши, нетрудно доказать интегральную формулу Коши: если функция f моногенна в области D и Г — простая замкнутая кривая, принадлежащая области D вместе со своей внутренностью D Гто для любой точки z Î D Г

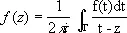
(ориентация кривой Г предполагается положительной относительно области D Г)

Пусть функция f моногенна в области D. Фиксируем произвольную точку z 0 области D и обозначим через g окружность с центром в точке z 0 и радиусом r > 0, принадлежащую, вместе со всем кругом: К: Iz - z 0I < r, области D. Тогда

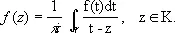
Представим ядро Коши 1/( t —z ) для t Îg и z Î K в виде суммы бесконечной геометрической прогрессии:

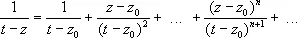
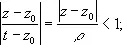
поэтому ряд сходится равномерно относительно t Îg при любом фиксированном z Î K, интегрируя этот ряд — после умножения на

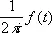
— почленно, получают разложение функции f в степенной ряд

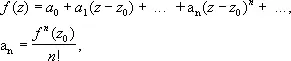
сходящийся в круге K: I z - z 0I < r.

Уточним теперь понятие аналитичности. Пусть f — функция, определённая в области D; она называется аналитической (или голоморфной) в точке z 0области , если существует окрестность этой точки (круг с центром в z 0), в которой функция f представляется степенным рядом:

f ( z ) = a 0+ a 1( z - z 0) + a 2( z - z 0) 2+. . . . + a n( z - z 0) n+ . . .

Если это свойство имеет место в каждой точке z 0области D, то функция f называется аналитической (голоморфной) в области D.

Выше было показано, что функция f , моногенная в области D, аналитична в этой области. В отдельной точке это утверждение неверно; например, функция f ( z ) = êzê 2= z 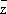моногенна в точке z 0= 0, но нигде не аналитична. С другой стороны, функция f , аналитическая в точке z 0области D, моногенна в этой точке. Более того, сумма сходящегося степенного ряда имеет производные всех порядков (бесконечно дифференцируема) по комплексному переменному z ; коэффициенты ряда могут быть выражены через производные функции f в точке z 0по формулам: a n= f (n)( z 0)/ n ! . Степенной ряд, записанный в форме

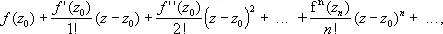
называется рядом Тейлора функции f в точке z 0. Тем самым, аналитичность функции f в области D означает, что в каждой точке области D функция f бесконечно дифференцируема и её ряд Тейлора сходится к ней в некоторой окрестности этой точки.

Следовательно, понятия моногенности и аналитичности функции в области тождественны и каждое из следующих свойств функции f в области D — моногенность, дифференцируемость в смысле комплексного анализа, дифференцируемость в смысле действительного анализа вместе с выполнением уравнений Коши — Римана — может служить определением аналитичности f в этой области.

Важнейшее свойство А. ф. выражается следующей теоремой единственности: две функции, аналитические в области D и совпадающие на каком-либо множестве, имеющем предельную точку в D, совпадают и во всей области D (тождественны). В частности, аналитическая в области функция, отличная от тождественного нуля, может иметь в области лишь изолированные нули.

Если Е — произвольное множество (в комплексной плоскости и, в частности, на действительной прямой), то функция f (z), z Î E, называется аналитической на множестве E, если каждая точка этого множества имеет окрестность, на пересечении которой с множеством Е функция f представляется сходящимся степенным рядом; это означает в действительности, что f аналитична на некотором открытом множестве, содержащем Е (точнее, существует открытое множество, содержащее Е, и аналитическая на нём функция, f совпадающая с f на множестве E ) . Для открытых множеств понятие аналитичности совпадает с понятием дифференцируемости по множеству (моногенности). Однако в общем случае это не так; в частности, на действительной прямой существуют функции, не только имеющие производную, но и бесконечно дифференцируемые в каждой точке, которые не являются аналитическими ни в одной точке этой прямой. Например,

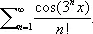
С другой стороны, для справедливости теоремы единственности А. ф. существенно свойство связности множества E. Поэтому А. ф. рассматриваются обычно в областях, т.е. на открытых и связных множествах.

Важную роль в изучении А. ф. играют точки, в которых нарушается свойство аналитичности — т. н. особые точки А. ф. Рассмотрим здесь изолированные особые точки (однозначных) А. ф. Пусть f — А. ф. в области вида 0 < | z - z 0| < r; в этой области f разлагается в ряд Лорана:

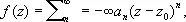
содержащий, вообще говоря, не только положительные, но и отрицательные степени z - z 0. Если в этом разложении члены с отрицательными степенями отсутствуют ( a n= 0 для n = -1, -2,...), то z 0 называется правильной точкой f . В правильной точке существует и конечен