БСЭ - Большая Советская энциклопедия (АН)

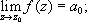
полагая f ( z 0) = a 0 , получают функцию, аналитическую во всём круге ïz - z 0ï < r .

Если ряд Лорана функции f содержит лишь конечное число членов с отрицательными степенями z - z 0 :

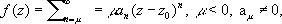
то точка z 0называется полюсом функции f (порядка m); полюс z 0 характеризуется тем, что

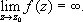
В случае, если ряд Лорана содержит бесконечное число отрицательных степеней z — z 0 , то z 0 называется существенно особой точкой; в таких точках не существует ни конечного, ни бесконечного предела функции f . Если z 0 — изолированная особая точка функции f, то коэффициент a -1в её разложении в ряд Лорана называется вычетом функции f в точке z 0.

Функции, представимые в виде отношения двух функций, аналитических в области D, называется мероморфными в области D. Мероморфная в области функция аналитична в этой области за исключением, быть может, конечного или счётного множества полюсов; в полюсах значения мероморфной функции считаются равными бесконечности. Если допустить такие значения, то мероморфные в области D функции могут быть определены как функции, которые в окрестности каждой точки z 0 области D представимы рядом по степеням z — z 0, содержащим конечное (зависящее от z 0 ) число членов с отрицательными степенями z — z 0.

Часто аналитическими в области D называют как аналитические (голоморфные), так и мероморфные в этой области функции. В этом случае голоморфные функции называют также регулярными аналитическими или просто регулярными. Простейший класс А. ф. составляют функции, аналитические во всей плоскости; такие функции называют целыми. Целые функции представляются рядами вида

a 0+ a 1 z + a 2 z 2+ ... + a n z n+...,

сходящимися во всей комплексной плоскости. К ним относятся многочлены от z , функции

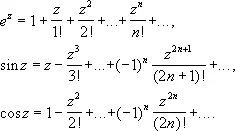
Функции, мероморфные во всей плоскости (т. е. представимые в виде отношения целых функций), называются мероморфными функциями. Таковыми являются рациональные функции от z (отношения многочленов),

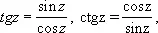
эллиптические функции и т. д.

Для изучения А. ф. важное значение имеют связанные с ними геометрические представления. Функцию w = f ( z ) , z ( D можно рассматривать как отображение области D в плоскость переменного w . Если f есть А. ф., то образ f ( D ) области D также является областью (принцип сохранения области). Из условия комплексной дифференцируемости функции f в точке z 0Î D следует, что при f’(z 0) ¹ 0 соответствующее отображение сохраняет углы в z 0, как по абсолютному значению, так и по знаку, т. е. является конформным. Т.о., существует тесная связь между аналитичностью и важным геометрическим понятием конформного отображения. Если f аналитична в D и f ( z ¢) ¹ f ( z ¢¢) при z ¢ ¹ z ¢¢ (такие функции называются однолистными), то f ¢ ( z ) ¹ 0 в D и f определяет взаимно однозначное и конформное отображение области D на область G = f ( D ) . Теорема Римана — основная теорема теории конформных отображений — утверждает, что в любой односвязной области, граница которой содержит более одной точки, существуют однолистные А. ф., конформно отображающие эту область на круг или полуплоскость.

Дифференцируя уравнения Коши — Римана, нетрудно усмотреть, что действительная и мнимая части функции f = j +i y , аналитичны в области D, удовлетворяют в этой области уравнению Лапласа:

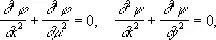
т. е. являются гармоническими функциями. Две гармонические функции, связанные между собой уравнениями Коши — Римана, называются сопряжёнными. В односвязной области D любая гармоническая функция j имеет сопряжённую функцию y и является, тем самым, действительной частью некоторой аналитической в D функции f . Связи с конформными отображениями и гармоническими функциями лежат в основе многих приложений теории А. ф.

Всё сказанное выше относилось к однозначным А. ф. f рассматриваемым в данной области D комплексной плоскости. Задаваясь вопросом о возможности продолжения функции f как А. ф. в большую область, приходят к понятию А. ф., рассматриваемой в целом — во всей своей естественной области существования. При таком продолжении данной функции область её аналитичности, расширяясь, может налегать сама на себя, доставляя новые значения функции в точках плоскости, где она уже была определена. Поэтому А. ф., рассматриваемая в целом, вообще говоря, оказывается многозначной. К необходимости изучения многозначных А. ф. приводят многие вопросы теории функций (обращение функций, нахождение первообразных и построение А. ф. с заданной действительной частью — в многосвязных областях, решение алгебраических уравнений с аналитичными коэффициентами и др.); такими функциями являются

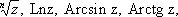
алгебраические функции и т. д. Регулярный процесс, приводящий к полной А. ф., рассматриваемой в своей естественной области существования, был указан К. Вейерштрассом; он носит название аналитического продолжения по Вейерштрассу.

Исходным является понятие элемента А. ф. — степенного ряда с ненулевым радиусом сходимости. Такой элемент W 0: a 0+ a 1(z - z 0) + a 2(z - z 0) 2+ ... + a n(z - z 0) n+ ... определяет некоторую А. ф. f в своём круге сходимости K 0. Пусть z 1— точка круга K 0 , отличная от z 0. Разлагая функцию f в ряд Тейлора с центром в точке z 1, получают новый элемент W 1:

b 0+ b 1( z - z 1) + b 2( z- z 1) 2+ ... +b n( z— z 1) n+ ... ,

круг сходимости которого обозначают через K 1 . В общей части кругов K 0и K 1ряд W 1сходится к той же функции, что и ряд W 0. Если круг K 1выходит за пределы круга K 0, то ряд W 1определяет функцию, заданную посредством W 0, на некотором множестве вне K 0(где ряд W 0расходится). В этом случае элемент W 1называется непосредственным аналитичным продолжением элемента W 0. Пусть W 0, W 1..., W N— цепочка элементов такая, что W i+1является непосредственным аналитичным продолжением W i(i = 1, ..., N — 1); тогда элемент W Nназывается аналитичным продолжением элемента W 0(посредством данной цепочки элементов). Может оказаться так, что центр круга K Nпринадлежит кругу K 0 , но элемент W Nне является непосредственным аналитичным продолжением элемента W 0. В этом случае суммы рядов W 0и W Nв общей части кругов K 0и K N имеют различные значения; тем самым аналитичное продолжение может привести к новым значениям функции в круге K 0 .