БСЭ - Большая Советская энциклопедия (АН)

Совокупность всех элементов, которые могут быть получены аналитичным продолжением элемента W 0, образует полную А. ф. (в смысле Вейерштрасса), порожденную элементом W 0; объединение их кругов сходимости представляет собой (вейерштрассову) область существования этой функции. Из теоремы единственности А. ф. следует, что А. ф. в смысле Вейерштрасса полностью определяется заданием элемента W 0При этом в качестве исходного может быть взят любой др. элемент, принадлежащий этой функции; полная А. ф. от этого не изменится.

Полная А. ф. f , рассматриваемая как функция точек плоскости, принадлежащих её области существования D, вообще говоря, является многозначной. Чтобы избавиться от многозначности, функцию f рассматривают не как функцию точек плоской области D, а как функцию точек некоторой (лежащей над областью D ) многолистной поверхности R такой, что каждой точке области D соответствует столько (проектирующихся в неё) точек поверхности R, сколько различных значений принимает функция f в этой точке: на поверхности R функция f становится однозначной функцией. Идея перехода к таким поверхностям принадлежит Б. Риману, а сами они называются римановы поверхности. Схематическое изображение римановых поверхностей функций 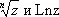приведены на рис. 1 и 2 (соответственно). Абстрактное определение понятия римановой поверхности позволило заменить теорию многозначных А. ф. теорией однозначных А. ф. на римановых поверхностях.

Фиксируем область D, принадлежащую области существования D полной А. ф. f , и какой-либо элемент W функции f с центром в точке области D. Совокупность всех элементов, которые могут быть получены аналитичным продолжением элемента W посредством цепочек, центры которых принадлежат D, называется ветвью А. ф. f . Ветвь многозначной А. ф. может оказаться однозначной А. ф. в области D. Так, например, произвольные ветви функций 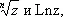соответствующие любой односвязной области, не содержащей точку O, являются однозначными функциями; при этом 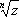имеет ровно n, a Lnz — бесконечное множество различных ветвей в каждой такой области. Выделение однозначных ветвей (с помощью тех или иных разрезов области существования) и их изучение средствами теории однозначных А. ф. являются одним из основных приёмов исследования конкретных многозначных А. ф.

Понятие А. ф. нескольких переменных вводится с помощью кратных степенных рядов — совершенно аналогично тому, как это было сделано выше для А. ф. одного переменного. А. ф. нескольких комплексных переменных по своим свойствам также во многом аналогичны А. ф. одного комплексного переменного; однако они обладают и рядом принципиально новых свойств, не имеющих аналогов в теории А. ф. одного переменного. Более общим является понятие А. ф. на комплексных многообразиях (понятие комплексного многообразия является обобщением понятия римановой поверхности для многомерного случая).

Лит.: Привалов И. И., Введение в теорию функций комплексного переменного, 11 изд., М., 1967; Смирнов В. И., Курс высшей математики, 8 изд., т. 3, ч. 2, М.—Л., 1969; Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1—2, М., 1967—68; Лаврентьев М. А., Шабат Б. В., Методы теории функций комплексного переменного, 3 изд., М., 1965; Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; Евграфов М. А., Аналитические функции, 2 изд., М., 1968; Свешников А. Г., Тихонов А. Н., Теория функций комплексной переменной, М., 1967; Фукс Б. А., Теория аналитических функций многих комплексных переменных, 2 изд., М., 1963; Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964; Маркушевич А. И., Очерки по истории теории аналитических функций, М.— Л., 1951; Математика в СССР за тридцать лет, 1917 — 1947, М.— Л., 1948, с. 319—414; Математика в СССР за сорок лет, 1917 — 1957, т. 1, М., 1959, с. 381—510.

А. А. Гончар.

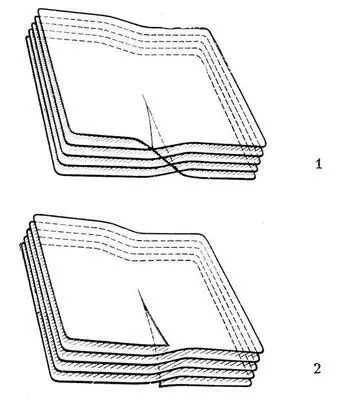
Рис. 1 и 2 к ст. Аналитические функции.

Аналити'ческие языки',тип языков, в которых грамматические отношения выражаются служебными словами, порядком слов, интонацией и т. п., а не словоизменением, т. е. не грамматическим чередованием морф в пределах словоформы, как в синтетических языках. К А. я. относятся английский, французский, новоперсидский, болгарский языки. Однако практически не существует ни чисто А. я., ни чисто синтетических (см. Синтетические языки ) . В А. я. чередование морф в пределах словоформы сохраняется в системе спряжения и частично склонения. Например, во французском языке je parle — «я говорю», но nous parlons — «мы говорим», в английском языке I work — «я работаю», но I worked — «я работал». В синтетических языках распространены и аналитические конструкции. В процессе исторического развития языков в А. я. образуются новые флективные формы, а в синтетических языках флективные формы вытесняются аналитическими конструкциями. Деление языков на аналитические и синтетические основывается на той или иной преобладающей языковой тенденции, характерной для морфологической структуры словоформы.

Аналити'ческий учёт, система бухгалтерских записей, дающая детальные сведения о движении хозяйственных средств; предназначается для оперативного руководства хозяйством и составления отчётности; строится по каждому синтетическому счёту в отдельности. Наиболее укрупнённые и общие для всех предприятий отрасли позиции А. у. предусматриваются в плане счетов и называются субсчетами. В отличие от синтетического учёта, А. у. ведётся не только в стоимостных, но и в натуральных показателях, а также содержит справочные данные. По синтетическим счетам с наиболее расчленённой системой записей для А. у. применяют отдельные учётные регистры (картотеки, ведомости и др.) — для пообъектного учёта основных средств по видам их и местам нахождения, складского количественно-сортового учёта материалов и готовой продукции, для лицевых счетов расчётов с рабочими и служащими по заработной плате, для учёта затрат в разрезе аналитических позиций калькуляционных счетов производства — по видам продукции, стадиям обработки, статьям калькуляции т. п. Записи А. у. по таким счетам сверяют с записями синтетического учёта посредством сальдовых либо оборотных ведомостей, итоги которых должны быть тождественны итогам записей в соответствующем синтетическом счёте. При менее разветвленной номенклатуре аналитических позиций — по фондовым, собирательно-распределительным счетам, большинству расчётных счетов — записи А. у. совмещают в общих регистрах с записями синтетического учёта (накопительных ведомостях, журналах-ордерах, табуляграммах и др.). Записи А. у. в этих регистрах заменяют записи синтетического учёта либо служат основанием для них. Достоверность показателей А. у. периодически проверяют путём инвентаризации .