БСЭ БСЭ - Большая Советская Энциклопедия (ВА)

Пусть x ( t ) — функция, удовлетворяющая условию (2), a h (t) — произвольная гладкая функция, удовлетворяющая условию h (t o) = h (T) = 0. Тогда величина

J (x + eh) = J*(e),

где e — произвольное действительное число будет функцией e . Вариацией dJ функционала J называют производную

(dJ*/de) e= 0.

Для простейшей задачи В. и.

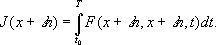
Разлагая полученное выражение в ряд по степеням e, получим

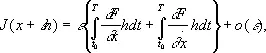
где о (e) — члены более высокого порядка. Так как h ( t o ) = h ( T ) = 0, то, проведя интегрирование по частям во втором интеграле, найдём

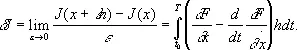
Пусть теперь x ( t ) реализует экстремум. Тогда функция J*(e) имеет экстремум при e = 0. Поэтому величина dJ должна обратиться в нуль. Отсюда следует: для того чтобы функция x ( t ) доставляла экстремум функционалу (1), необходимо, чтобы она удовлетворяла уравнению

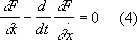
называемому уравнением Эйлера.

Это — дифференциальное уравнение 2-го порядка относительно функции x ( t ) . Необходимое условие dJ = 0 может быть применено в ряде случаев для эффективного отыскания решения вариационной задачи, поскольку функция x ( t ) необходимо должна быть решением краевой задачи x ( t o ) = x o, x ( T ) = x T для уравнения (4). Если найдено это решение и оно единственно, то найдено тем самым и решение исходной вариационной задачи. Если краевая задача допускает несколько решений, то достаточно вычислить значение функционала для каждого из решений краевой задачи и выбрать из них то, которому отвечает наименьшее значение J ( x ) . Однако указанный путь обладает одним существенным недостатком: не существует универсальных способов решения краевых задач для обыкновенных (нелинейных) дифференциальных уравнений.

Уже во 2-й половине 18 в. круг задач, изучаемых В. и., значительно расширился. Прежде всего основные результаты, относящиеся к простейшей задаче В. и., были перенесены на общий случай интегральных функционалов вида

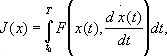
где x ( t ) — вектор-функция произвольной размерности, и на функционалы ещё более общего вида.

Условный экстремум. Задача Лагранжа.В конце 18 в. был сформулирован ряд задач на условный экстремум. Этим термином принято называть задачи отыскания функции x ( t ) , доставляющей экстремум функционалу J ( x ) при каких-либо дополнительных условиях, кроме условий на концах интервала (t 0, T). Простейшей задачей подобного вида является класс так называемых изопериметрических задач. Своим названием этот класс задач обязан следующей: среди всех замкнутых кривых данной длины найти ту, которая ограничивает максимальную площадь.

Значительно более сложной задачей является та, в которой ограничения носят характер дифференциальных уравнений. Эту задачу называют задачей Лагранжа; особое значение она приобрела в середине 20 в. в связи с созданием теории оптимального управления. Поэтому её формулировка даётся ниже на языке этой теории, возникшем после работ Л. С. Понтрягина и его учеников.

Пусть x (t) и u (t) — вектор-функции размерностей n и m соответственно, причём функция x ( t ) , которую называют фазовым вектором, при t = t o и t = T удовлетворяет граничным условиям:

x (t 0) Î e 0, x (T) Î e T (5)

где e 0и e T— некоторые множества. Простейшим примером условий типа (5) являются условия (2). Функция x ( t ) и функция u ( t ) , которую называют управлением, связаны условием

dx/dt = f (x, u, t), (6)

где f — дифференцируемая вектор-функция своих аргументов. Рассматриваемая задача состоит в следующем: определить функции x ( t ) и u ( t ) , доставляющие экстремум функционалу

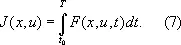
Заметим, что и простейшая задача В. и. и изопериметрическая задача являются частным случаем задачи Лагранжа.

Задача Лагранжа имеет огромное прикладное значение. Пусть, например, уравнение (6) описывает движение какого-либо динамического объекта, например космического корабля. Управление u — это вектор тяги его двигателя. Множества e 0 и e T — это две орбиты разных радиусов. Функционал (7) описывает расход горючего на выполнение маневра. Следовательно, задачу Лагранжа, применительно к данной ситуации, можно сформулировать следующим образом: определить закон изменения тяги двигателя космического аппарата, совершающего переход с орбиты e 0 на орбиту e T за заданное время так, чтобы расход топлива на этот маневр был минимальным.

Важную роль в теории подобных задач играет функция Гамильтона

H (x, y, u) = (f, y) - F.

Здесь y — вектор, называется множителем Лагранжа (или импульсом), (f, y) означает скалярное произведение векторов f и y . Необходимое условие в задаче Лагранжа формулируется следующим образом: для того чтобы функци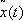и и 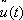были решением задачи Лагранжа, необходимо, чтобы 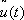была стационарной точкой функции Гамильтона Н (х, y, u), то есть, чтобы при

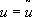
было ¶ H/ ¶ u = 0, где y — не равное тождественно нулю решение уравнения

¶y/t = —¶H/¶x = j(x, y, u, t). (8)

Эта теорема имеет важное прикладное значение, так как она открывает известные возможности для фактического нахождения векторов x ( t ) и u ( t ) .

Развитие В. и. в 19 в.Основные усилия математиков в 19 в. были направлены на исследование условий, необходимых или достаточных для того, чтобы функция x ( t ) реализовала экстремум функционала J ( x ) . уравнение Эйлера было первым из таких условий; оно аналогично необходимому условию

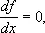
которое устанавливается в теории функций конечного числа переменных. Однако в этой теории известны ещё и другие условия. Например, для того, чтобы функция f ( x ) имела в точке 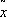минимум, необходимо, чтобы в этой точке было