БСЭ БСЭ - Большая Советская Энциклопедия (ВЕ)

x = a 1e 1 + a 2e 2 + ... + a ne n .

При этом числа a 1, a 2,..., a n называются координатами вектора х в данном базисе.

Примеры В. п.Множество всех векторов трёхмерного пространства образует, очевидно, В. п. Более сложным примером может служить так называемое n-мерное арифметическое пространство. Векторами этого пространства являются упорядоченные системы из n действительных чисел : l 1, l 2,..., l n. Сумма двух векторов и произведение на число определяются соотношениями:

( l 1, l 2, …, l n ) + ( m 1, m 2, …, m n ) = ( l 1 + m 1, l 2 + m 2, …, l n + m n ) ;

a ( l 1, l 2, …, l n ) = ( al 1, al 2, …, al n ) .

Базисом в этом пространстве может служить, например, следующая система из n векторов e 1 = (1, 0,..., 0), e 2 = (0, 1,..., 0),..., e n = (0, 0,..., 1).

Множество R всех многочленов a 0 + a 1u + … + a nu n (любых степеней n ) от одного переменного с действительными коэффициентами a 0, a 1,..., a n с обычными алгебраическими правилами сложения многочленов и умножения многочленов на действительные числа образует В. п. Многочлены 1, u, u 2,..., u n (при любом n ) линейно независимы в R, поэтому R — бесконечномерное В. п.

Многочлены степени не выше n образуют В. п. размерности n + 1 ; его базисом могут служить многочлены 1, u, u 2,..., u n.

Подпространства В. п.В .п. R' называется подпространством R, если R' Í R (то есть каждый вектор пространства R' есть и вектор пространства R ) и если для каждого вектора v Î r' и для каждых двух векторов v 1 и v 2 ( v 1, v 2Î R' ) вектор lv (при любом l ) и вектор v 1 + v 2 один и тот же независимо от того, рассматриваются ли векторы v, v 1, v 2 как элементы пространства R' или R. Линейной оболочкой векторов x 1, x 2,... x p называется множество всевозможных линейных комбинаций этих векторов, то есть векторов вида a 1x 1 + a 2x 2 + … + a px p . В трёхмерном пространстве линейной оболочкой одного ненулевого вектора x 1 будет, очевидно, совокупность всех векторов, лежащих на прямой, определяемой вектором x 1. Линейной оболочкой двух не лежащих на одной прямой векторов x 1 и x 2 будет совокупность всех векторов, расположенных в плоскости, которую определяют векторы x 1 и x 2. В общем случае произвольного В. п. R линейная оболочка векторов x 1, x 2,..., x p этого пространства представляет собой подпространство пространства R размерности р. В n-мерном В. п. существуют подпространства всех размерностей, меньших р. Всякое конечномерное (данной размерности k ) подпространство R' В. п. R есть линейная оболочка любых k линейно независимых векторов, лежащих в R'. Пространство, состоящее из всех многочленов степени £ n (линейная оболочка многочленов 1, u, u 2,..., u n ) , есть ( n + 1 ) - мepное подпространство пространства R всех многочленов.

Евклидовы пространства.Для развития геометрических методов в теории В. п. нужно указать пути обобщения таких понятий, как длина вектора, угол между векторами и т.п. Один из возможных путей заключается в том, что любым двум векторам х и у из R ставится в соответствие число, обозначаемое ( х, у ) и называемое скалярным произведением векторов х и у. При этом требуется, чтобы выполнялись следующие аксиомы скалярного произведения:

1) ( х, у ) = ( у, х ) (перестановочность);

2) ( x 1 + x 2, y ) = ( x 1, y ) + ( x 2, y ) (распределительное свойство);

3) ( ax, у ) = a ( х, у ) ,

4) ( х, х ) ³ 0 для любого х , причем ( х, х ) = 0 только для х = 0 .

Обычное скалярное произведение в трёхмерном пространстве этим аксиомам удовлетворяет. В. п., в котором определено скалярное произведение, удовлетворяющее перечисленным аксиомам, называется евклидовым пространством; оно может быть как конечномерным (n-мерным), так и бесконечномерным. Бесконечномерное евклидово пространство обычно называют гильбертовым пространством. Длина | x | вектора x и угол 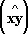между векторами х и у евклидова пространства определяются через скалярное произведение формулами

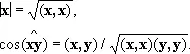
Примером евклидова пространства может служить обычное трёхмерное пространство со скалярным произведением, определяемым в векторном исчислении. Евклидово n-мepное (арифметическое) пространство E n получим, определяя в n -мepном арифметическом В. п. скалярное произведение векторов x = ( l 1, …, l n ) и y = ( m 1, …, m n ) соотношением

( x, y ) = l 1m 1 + l 2m 2 + … + l nm n. (2)

При этом требования 1)—4), очевидно, выполняются.

В евклидовых пространствах вводится понятие ортогональных (перпендикулярных) векторов. Именно векторы х и у называются ортогональными, если их скалярное произведение равно нулю: ( х, у ) = 0. В рассмотренном пространстве E n условие ортогональности векторов x = ( l 1, …, l n ) и y = ( m 1, …, m n ) , как это следует из соотношения (2), имеет вид:

l 1m 1 + l 2m 2 + … + l nm n = 0. (3)

Применение В. п. Понятие В. п. (и различные обобщения) широко применяется в математике и её приложениях к естествознанию. Пусть, например, R — множество всех решений линейного однородного дифференциального уравнения y n + a 1 ( x ) y ( n + 1 )+ … + a n ( x ) y = 0 . Ясно, что сумма двух решений и произведение решения на число являются решениями этого уравнения. Таким образом, R удовлетворяет условиям А. Доказывается, что для R выполнено обобщённое условие В. Следовательно, R является В. п. Любой базис в рассмотренном В. п. называется фундаментальной системой решений, знание которой позволяет найти все решения рассматриваемого уравнения. Понятие евклидова пространства позволяет полностью геометризовать теорию систем однородных линейных уравнений:

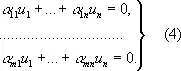
Рассмотрим в евклидовом пространстве E n векторы a i = ( a i1, a i2, …, a in ) , i = 1, 2,..., n и вектор-решение u = ( u 1, u 2,..., u n ). Пользуясь формулой (2) для скалярного произведения векторов E n, придадим системе (4) следующий вид:

( a i, u ) = 0, i = 1, 2, …, m . (5)

Из соотношений (5) и формулы (3) следует, что вектор-решение u ортогонален всем векторам a i. Иными словами, этот вектор ортогонален линейной оболочке векторов a i, то есть решение u есть любой вектор из ортогонального дополнения линейной оболочки векторов a i . Важную роль в математике и физике играют и бесконечномерные линейные пространства. Примером такого пространства может служить пространство С непрерывных функций на отрезке с обычной операцией сложения и умножения на действительные числа. Упомянутое выше пространство всех многочленов является подпространством пространства С .