БСЭ БСЭ - Большая Советская Энциклопедия (ВЕ)

[ a, b ] = — [ b, а ] , [( l a ) , b ] = l [ a, b ] ,

[ с, ( a + b )] = [ с, a ] + [ с, b ] , [ a, [ b, с ]] = b ( a, с ) — с ( a, b ) ,

([ a, b ] , [ с, d ]) = ( a, c )( b, d ) — ( a, d )( b, c ) .

Если в ортонормированном базисе i, j, k, образующем правую тройку, векторы a и b имеют соответственно координаты í X 1, Y 1, Z 1 ý и í X 2, Y 2, Z 2 ý , то [ a, b ] = í Y 1Z 2— Y 2Z 1 , Z 1X 2— Z 2X 1, X 1Y 2— X 2Y 1 ý. Понятие векторного произведения связано с различными вопросами механики и физики. Например, скорость v точки М тела, вращающегося с угловой скоростью со вокруг оси l, равна [ w, r ] , где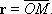

Смешанным произведением векторов a, bи cназывается скалярное произведение вектора [ a, b ] на вектор с: ([ a, b ] , с ) . Обозначается смешанное произведение символом abc .Смешанное произведение не параллельных одной плоскости векторов a, b и с численно равно объёму параллелепипеда, построенного на приведённых к общему началу векторах a, b и с , взятому со знаком плюс, если тройка a, b и с правая, и со знаком минус, если тройка левая. Если же векторы a, b и с параллельны одной плоскости, то abc = 0 . Справедливо также следующее свойство abc = bca = cab . Если координаты векторов a, b и с в ортонормированном базисе i, j, k, образующем правую тройку, соответственно равны í X 1, Y 1, Z 1 ý , í X 2, Y 2, Z 2 ý и í Х 3, Y 3, Z 3 ý, то

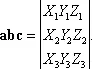
Вектор-функции скалярных аргументов.В механике, физике, дифференциальной геометрии широко используется понятие вектор-функции одного или нескольких скалярных аргументов. Если каждому значению переменной t из некоторого множества í t ý ставится в соответствие по известному закону определённый вектор r, то говорят, что на множестве í t ý задана вектор-функция (векторная функция) r = r ( t ) . Так как вектор r определяется координатами í x, y, z ý, то задание вектор-функции r = r ( t ) эквивалентно заданию трёх скалярных функций: х = x ( t ) , y = y ( t ) , z = z ( t ). Понятие вектор-функции становится особенно наглядным, если обратиться к так называемому годографу этой функции, то есть к геометрическому месту концов всех векторов r ( t ) , приложенных к началу координат О ( рис. 7 ). Если при этом рассматривать аргумент t как время, то вектор-функция r ( t ) представляет собой закон движения точки М, движущейся по кривой L — годографу функции r ( t ) .

Для изучения вектор-функций важную роль играет понятие производной. Это понятие вводится следующим образом: аргументу t придаётся приращение Dt ¹ 0 и вектор D r = r ( t + Dt ) — r ( t ) ( на рис. 7 это вектор 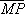) множится на 1/Dt . Предел выражения D r/Dt при Dt ® 0 называется производной вектор-функции r ( t ) и обозначается r' ( t ) или d r/dt . Производная представляет собой вектор, касательный к годографу L в данной точке М. Если вектор-функция рассматривается как закон движения точки по кривой L, то производная r' ( t ) равна скорости движения этой точки. Правила вычисления производных различных произведений вектор-функций подобны правилам вычисления производных произведений обычных функций. Например,

( r 1, r 2 ) ' = ( r' 1, r 2 ) + ( r 1, r' 2 ) ,

[ r 1, r 2 ] ’ = [ r' 1, r 2 ] + [ r 1, r' 2 ] .

В дифференциальной геометрии вектор-функции одного аргумента используются для задания кривых. Для задания поверхностей пользуются вектор-функциями двух аргументов.

Векторный анализ.В механике, физике и геометрии широко используются понятия скалярного и векторного поля. Температура неравномерно нагретой пластинки, плотность неоднородного тела представляют собой физические примеры соответственно плоского и пространственного скалярного поля. Векторное поле образует множество всех векторов скоростей частиц установившегося потока жидкости. Примерами векторных полей могут служить также поле силы тяжести, магнитное и электрическое напряжение электромагнитного поля.

Для математического задания скалярных и векторных полей используются соответственно скалярные и векторные функции. Ясно, что плотность тела представляет собой скалярную функцию точки, а поле скоростей частиц установившегося потока жидкости — векторную функцию точки. Математический аппарат теории поля обычно называют векторным анализом. Для геометрической характеристики скалярного поля используются понятия линий и поверхностей уровня. Линией уровня плоского скалярного поля называется линия, на которой функция, задающая поле, имеет постоянное значение. Аналогично определяется поверхность уровня пространственного поля. Примерами линии уровня могут служить изотермы — линии уровня скалярного поля температур неравномерно нагретой пластинки.

Обратимся к поверхности (линии) уровня скалярного поля, проходящей через данную точку М. При смещении по нормали к этой поверхности (линии) в точке М наблюдается максимальное изменение в этой точке функции f задающей поле. Это изменение характеризуется с помощью градиента скалярного поля. Градиент представляет собой вектор, направленный по нормали к поверхности (линии) уровня в точке М в сторону возрастания f этой точке. Величина градиента равна производной f указанном направлении. Обозначается градиент символом grad f . В базисе i, j k градиент grad f имеет координаты