БСЭ БСЭ - Большая Советская Энциклопедия (ВЕ)

называемое формулой Стокса. Формула (2) выражает следующий физический факт: поток вихря векторного поля а через поверхность Г равен циркуляции этого поля вдоль кривой g. Формула Остроградского служит источником инвариантного (независящего от выбора системы координат) определения основных операций векторного анализа. Например, из этой формулы вытекает, что

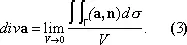
Так как выражение

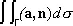
представляет собой поток жидкости через Г , а

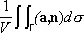
величину этого потока на единицу объёма, то определение div а с помощью соотношения (3) показывает, что div а характеризует интенсивность источника в данной точке.

Лит.: Кочин Н. Е., Векторное исчисление и начала тензорного исчисления, 6 изд., Л.—М., 1938; Дубнов Я. С., Основы векторного исчисления, 4 изд., т. 1—2, М., 1950—52; Будак Б. М., Фомин С. В., Кратные интегралы и ряды, 2 изд., М., 1967.

Э. Г. Позняк.

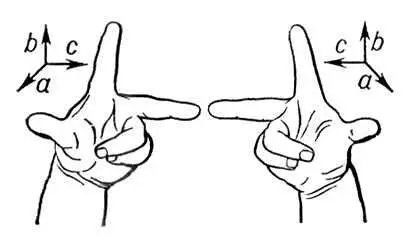
Рис. 6 к ст. Векторное исчисление.

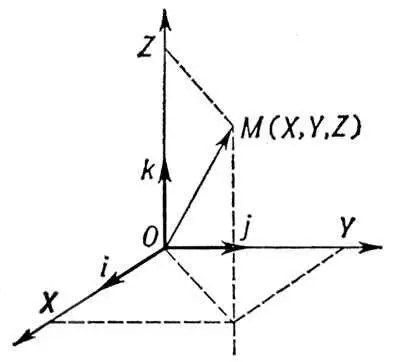
Рис. 5 к ст. Векторное исчисление.

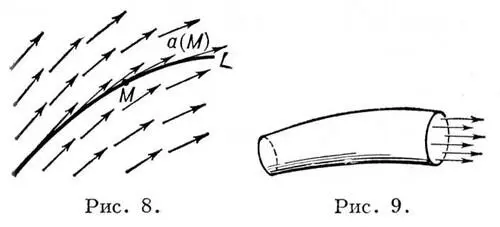
Рисунки 8, 9 к ст. Векторное исчисление.

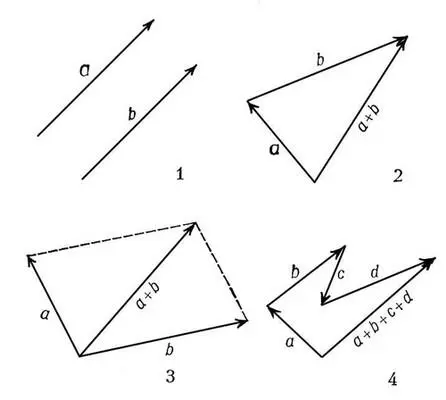
Рисунки 1—4 к ст. Векторное исчисление.

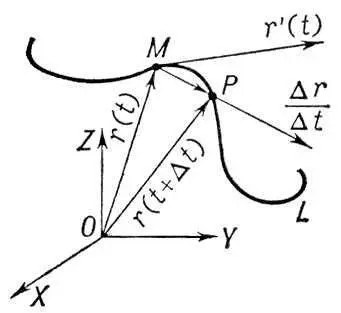
Рис. 7 к ст. Векторное исчисление.

Ве'кторное по'ле, область, в каждой точке Р которой задан вектор а ( Р ). Математически В. п. может быть определено в данной области G посредством вектор-функции a ( Р ) переменной точки Р этой области. К понятию В. п. приводит целый ряд физических явлений и процессов (например, векторы скоростей частиц движущейся жидкости в каждый момент времени образуют В. п.). Теория В. п. широко разработана и имеет разнообразные применения в различных областях естествознания (см. Векторное исчисление ) .

Лит.: Будак Б. М.. Фомин С. В., Кратные интегралы и ряды, 2 изд., М., 1967.

Э. Г. Позняк.

Ве'кторное произведе'ниевектора а на вектор b — вектор, обозначаемый [ а, b ] и определяемый так: 1) длина вектора [ а, b ] равна произведению длин векторов а и b на синус угла j между ними (берётся тот из двух углов между а и b , который не превосходит p ), 2) вектор [ а, b ] перпендикулярен вектору а и вектору b , 3) тройка векторов а, b , [ а, b ], согласно с ориентацией пространства, всегда правая или всегда левая (см. Векторное исчисление ) . В. п. широко применяется в геометрии, механике и физике (например, момент силы F, приложенной к точке М относительно точки О , есть В. п. [ 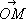, F ]).

Лит.; Ильин В. А., Позняк Э. Г., Аналитическая геометрия, М., 1968.

Э. Г. Позняк.

Ве'кторное простра'нство,математическое понятие, обобщающее понятие совокупности всех (свободных) векторов обычного трёхмерного пространства.

Определение В. п.Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действительные числа (см. Векторное исчисление ) . В применении к любым векторам х, у, z и любым числам a, b эти правила удовлетворяют следующим условиям (условия А):

1) х + у = у + х (перестановочность сложения);

2) ( х + у ) + z = x + ( y + z ) (ассоциативность сложения);

3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x + 0 = x: для любого вектора x ;

4) для любого вектора х существует противоположный ему вектор у такой, что х + у = 0 ,

5) 1 · х = х,

6) a ( bx ) = ( ab ) х (ассоциативность умножения);

7) ( a + b ) х = aх + bх (распределительное свойство относительно числового множителя);

8) a ( х + у ) = aх + aу (распределительное свойство относительно векторного множителя).

Векторным (или линейным) пространством называется множество R, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные числа, удовлетворяющие условиям А (условия 1—3 выражают, что операция сложения, определённая в В. п., превращает его в коммутативную группу). Выражение

a 1e 1 + a 2e 2 + … + a ne n (1)

называется линейной комбинацией векторов e 1, e 2,..., e n с коэффициентами a 1, a 2 , ..., a n. Линейная комбинация (1) называется нетривиальной, если хотя бы один из коэффициентов a 1, a 2,..., a n отличен от нуля. Векторы e 1, e 2,..., e n называются линейно зависимыми, если существует нетривиальная комбинация (1), представляющая собой нулевой вектор. В противном случае (то есть если только тривиальная комбинация векторов e 1, e 2,..., e n равна нулевому вектору) векторы e 1, e 2,..., e n называется линейно независимыми.

Векторы (свободные) трёхмерного пространства удовлетворяют следующему условию (условие В): существуют три линейно независимых вектора; любые четыре вектора линейно зависимы (любые три ненулевых вектора, не лежащие в одной плоскости, являются линейно независимыми).

В. п. называется n-мepным (или имеет «размерность n» ) , если в нём существуют n линейно независимых элементов e 1, e 2,..., e n, а любые n + 1 элементов линейно зависимы (обобщённое условие В). В. п. называются бесконечномерным, если в нём для любого натурального n существует n линейно независимых векторов. Любые n линейно независимых векторов n-мepного В. п. образуют базис этого пространства. Если e 1, e 2,..., e n — базис В. п., то любой вектор х этого пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов: