БСЭ БСЭ - Большая Советская Энциклопедия (ВЕ)

В векторной алгебре важную роль играют линейные операции над векторами: операция сложения векторов и умножения вектора на действительное число. Суммой а + b векторов а и b называют вектор, идущий из начала вектора а в конец вектора b при условии, что начало вектора b приложено к концу вектора а ( рис. 2 ). Происхождение этого правила связано с правилом параллелограмма сложения векторов ( рис. 3 ), источником которого является экспериментальный факт сложения сил (векторных величин) по этому правилу. Построение суммы нескольких векторов ясно из рис. 4 . Произведением a а вектора ана число a называется вектор, коллинеарный вектору а, имеющий длину, равную l a l . l a l, и направление, совпадающее с направлением а при a > 0 и противоположное а при a < 0. Вектор —1 · а называется противоположным вектору а и обозначается — а. Операции сложения векторов и умножения вектора на число обладают следующими свойствами:

1) а + b = b + a,

2) ( a + b ) + c = a + ( b + c ) ,

3) а + 0 = а,

4) a + ( -a ) = 0,

5) 1 · a = a,

6) a ( b a ) = ( ab ) a,

7) a ( a + b ) = a а + a b,

8) ( a + b ) a = a a + b a .

В векторной алгебре часто используется понятие линейно зависимых и линейно независимых векторов. Векторы a 1, a 2, ..., a n называются линейно зависимыми, если найдутся такие числа a 1, a 2,..., a n из которых хотя бы одно отлично от нуля, что линейная комбинация ( a 1 a 1 + ... + a n a n ) этих векторов равна нулю. Векторы a 1, a 2,..., a n, не являющиеся линейно зависимыми, называются линейно независимыми. Отметим, что любые три ненулевых вектора, не лежащие в одной плоскости, являются линейно независимыми.

Векторы евклидова пространства обладают следующим свойством: существуют три линейно независимых вектора, любые же четыре вектора линейно зависимы. Это свойство характеризует трехмерность рассматриваемого множества векторов. В сочетании с перечисленными выше свойствами указанное свойство означает, что совокупность всех векторов евклидова пространства образует, так называемое, векторное пространство. Линейно независимые векторы e 2, e 2, e 3 , образуют базис. Любой вектор аможет быть единственным образом разложен по базису: а = X e 2 + Y e 2 + Z e 3 ; коэффициенты X, Y, Z называются координатами (компонентами) вектора а в данном базисе. Если вектор аимеет координаты X, Y, Z , то это записывают так: а = í X, Y, Z ý . Три взаимно ортогональных (перпендикулярных) вектора, длины которых равны единице и которые обычно обозначают так : i, j, k, образуют, так называемый ортонормированный базис. Если эти векторы поместить началами в одну точку О, то они образуют в пространстве декартову прямоугольную систему координат. Координаты X, Y, Z любой точки М в этой системе определяются как координаты вектора ОМ ( рис. 5 ). Указанным выше линейным операциям над векторами отвечают аналогичные операции над их координатами: если координаты векторов а и b равны соответственно í X 1, Y 1, Z 1 ý и í X 2, Y 2, Z 2 ý , то координаты суммы а + b этих векторов равны íX 1+ X 2, Y 1+ Y 2, Z 1+ Z 2ý, координаты вектора l a равны í lX 1 + lY 1 + lZ 1 ý .

Развитие и применение векторной алгебры тесно связано с различными типами векторных произведений: скалярного, векторного и смешанного. Понятие скалярного произведения векторов возникает, например, при рассмотрении работы силы F на заданном пути S : работа равна | F || S | cosj, где j — угол между векторами F и S. Математически скалярное произведение векторов а и b определяется как число, обозначаемое ( а, b ) и равное произведению длин этих векторов на косинус угла между ними:

( a, b ) = | a || b | cosj.

Величина | b | cosj называется проекцией вектора b на ось, определяемую вектором а, и обозначается пр ab . Поэтому ( a, b ) = | a | пр ab . В частности, если a — единичный вектор (| a | = 1 ) , то ( а, b ) = пр ab . Очевидны следующие свойства скалярного произведения:

( а, b ) = ( b, а ), ( l а, b ) = l ( а, b ) ,

( а + b, с ) = ( а, с ) + ( b, с ), ( a, а ) ³ 0,

причём равенство нулю имеет место лишь при a = 0 . Если в ортонормированном базисе i, j, k векторы а и b имеют соответственно координаты í X 1, Y 1, Z 1 ý и í Х 2, Y 2, Z 2 ý, то ( a, b ) = X 1X 2 + Y 1Y 2 + Z 1Z 2,

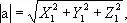
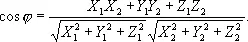
Для определения векторного произведения векторов нужно понятие левой и правой упорядоченной тройки векторов. Упорядоченная тройка векторов а, b, с ( а — первый вектор, b— второй , с — третий), приведённых к общему началу и не лежащих в одной плоскости, называется правой (левой), если они располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки. На рис. 6 изображены справа — правая, а слева — левая тройки векторов.

Векторным произведением векторов a и b называют вектор, обозначаемый [ a, b ] и удовлетворяющий следующим требованиям: 1) длина вектора [ a, b ] равна произведению длин векторов a и b на синус угла j между ними (таким образом, если a и b коллинеарны, то [ a, b ] = 0); 2) если a и b неколлинеарны, то [ a, b ] перпендикулярен каждому из векторов a и b и направлен так, что тройка векторов a , b, [ a, b ] является правой. Векторное произведение обладает следующими свойствами: