БСЭ БСЭ - Большая Советская Энциклопедия (ДИ)

Различные разделы Д. г. посвящены изучению во всевозможных аспектах так называемых дифференциально-геометрических многообразии . Примерами таких многообразий могут служить кривые (одномерные многообразия), поверхности (двумерные многообразия), обычное евклидово пространство (трёхмерное многообразие). Более сложным примером может служить четырёхмерное многообразие, элементами которого являются прямые обычного евклидова пространства (прямая в декартовых координатах определяется уравнениями вида z = ax + b , z = су + d ; числа a , b , с , d можно рассматривать как координаты этой прямой).

Изучение дифференциально-геометрических многообразий ведётся по следующим основным направлениям. 1) Геометрия транзитивной группы отображений многообразия на себя, или геометрия «локальной группы» отображений. В тематику этих вопросов входят обычная классическая локальная Д. г. (изучение инвариантов группы движений евклидова пространства), аффинная, проективная и конформная геометрии (изучение инвариантов соответствующей группы преобразований). 2) Геометрия многообразий с римановой метрикой ( римановых пространств ), представляющая собой обобщение на многомерный случай внутренней геометрии поверхностей, которое можно рассматривать как двумерные римановы пространства. Геометрия римановых пространств играет важную роль в теории относительности. 3) Геометрия так называемых финслеровых пространств, являющихся обобщением римановых пространств. 4) Геометрия многообразий со связностью, т. е. многообразий, в которых указан способ, с помощью которого можно сравнивать геометрические образы, расположенные в касательных пространствах в разных точках.

Возникновение Д. г. связано с именами Л. Эйлера и Г. Монжа . Ими к концу 18 в. были получены важные факты теории поверхностей. Значительный вклад в развитие Д. г. сделан в начале 19 в. К. Гауссом, который ввёл обе основные квадратичные формы. Им же была доказана теорема об инвариантности полной кривизны относительно изометрических преобразований. Фактически им были заложены основы внутренней геометрии поверхностей. Построение основ классической теории поверхностей было завершено в середине 19 в. основателем московской геометрической школы К. М. Петерсоном. В середине и во 2-й половине 19 в. много глубоких и общих результатов по классической теории поверхностей было получено Ф. Миндингом , Ж. Лиувиллем , Э. Бельтрами , Ж. Г. Дарбу , Л. Бианки . Ряд замечательных результатов по классической Д. г. был получен русскими учёными Д. Ф. Егоровым , Н. Н. Лузиным , С. П. Финиковым и др.

Развитие др. направлений в Д. г. связано с именами Б. Римана , Г. Ламе , Ф. Клейна , Г. Вейля , Э. Картана .

В СССР разрабатывались различные направления Д. г.; наибольшие успехи относятся к области проблем «в целом» (А. Д. Александров , А. В. Погорелов и др.).

Лит.: Монж Г., Приложение анализа к геометрии, пер. с франц., М. — Л., 1936; Стройк Д. Дж., Очерк истории дифференциальной геометрии до XX столетия, пер. с англ., М. — Л., 1941; Погорелов А. В., Дифференциальная геометрия, 5 изд., М., 1969; Рашевский П. К., Курс дифференциальной геометрии, 3 изд., М., 1950; Бляшке В., Введение в дифференциальную геометрию, пер. с нем., М., 1957; Рашевский П. К., Риманова геометрия и тензорный анализ, 2 изд., М., 1964; Александров А. Д., Внутренняя геометрия выпуклых поверхностей, М. — Л., 1948; Погорелов А. В., Внешняя геометрия выпуклых поверхностей, М., 1969.

Э. Г. Позняк.

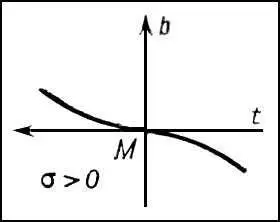
Рис. 6 к ст. Дифференциальная геометрия.

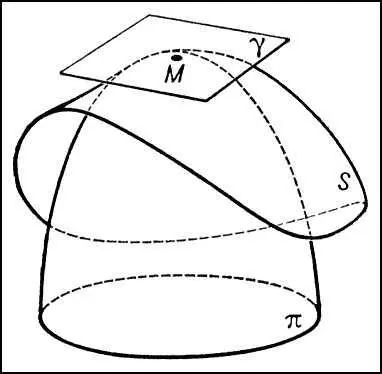
Рис. 7 к ст. Дифференциальная геометрия.

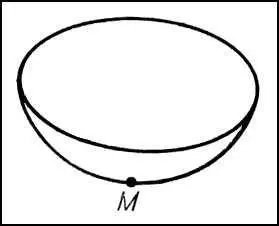
Рис. 8 к ст. Дифференциальная геометрия.

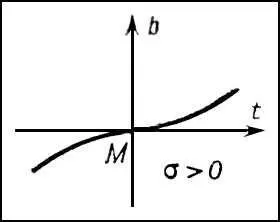
Рис. 5 к ст. Дифференциальная геометрия.

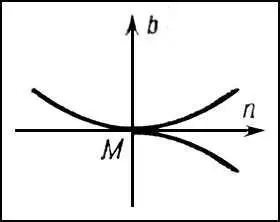
Рис. 4 к ст. Дифференциальная геометрия.

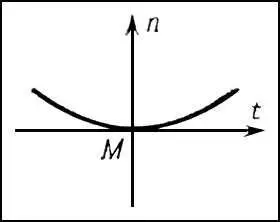
Рис. 3 к ст. Дифференциальная геометрия.

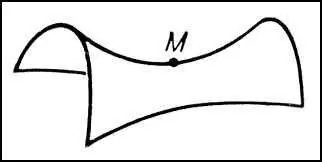
Рис. 9 к ст. Дифференциальная геометрия.

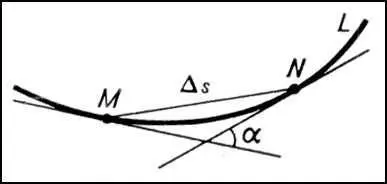
Рис. 2 к ст. Дифференциальная геометрия.

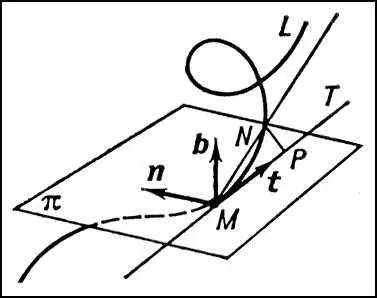
Рис. 1 к ст. Дифференциальная геометрия.

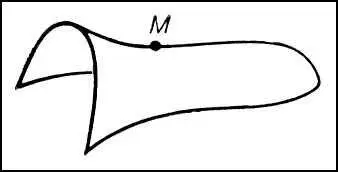
Рис. 10 к ст. Дифференциальная геометрия.

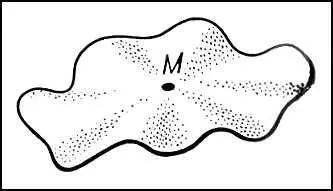
Рис. 11 к ст. Дифференциальная геометрия.

Рис. 12 к ст. Дифференциальная геометрия.

Дифференциа'льная психоло'гия,отрасль психологии , изучающая индивидуальные различия между людьми. Предпосылкой возникновения Д. п. на рубеже 19 и 20 вв. явилось введение в психологию эксперимента, а также генетических и математических методов. Пионером разработки Д. п. был Ф. Гальтон (Великобритания), который изобрёл ряд приёмов и приборов для изучения индивидуальных различий. В. Штерн (Германия) ввёл самый термин «Д. п.» (1900). Первыми крупными представителями Д. п. были А. Бине (Франция), А. Ф. Лазурский (Россия), Дж. Кеттел (США) и др.

В Д. п. широко применяются тесты — как индивидуальные, так и групповые; они используются для определения умственных различий, а с изобретением так называемых проективных тестов — для определения интересов, установок, эмоциональных реакций. С помощью тестов методами факторного анализа выявляются факторы, характеризующие общие свойства (параметры, измерения) интеллекта или личности. На этом основании определяются количественные вариации в психологических свойствах отдельных индивидов.