БСЭ БСЭ - Большая Советская Энциклопедия (ДИ)

В общем случае эти вычисления надо проводить для любого момента времени t , промежутка времени от t до t + D t и закона движения, выражаемого формулой s = f ( t ). Тогда средняя скорость движения за промежуток времени от t до t + D t даётся формулой Ds/D t , где D s = f ( t + D t ) — f ( t ), а скорость движения в момент времени t равна

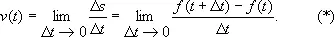
Основное преимущество скорости в данный момент времени, или мгновенной скорости, перед средней скоростью состоит в том, что она, как и закон движения, является функцией времени t , а не функцией интервала ( t , t + D t ). С другой стороны, мгновенная скорость представляет собой некоторую абстракцию, поскольку непосредственному измерению поддаётся средняя, а не мгновенная скорость.

К выражению типа (*) приводит и задача (см. рис. ) построения касательной к плоской кривой в некоторой её точке М . Пусть кривая Г есть график функции у = f ( x ). Положение касательной будет определено, если будет найден её угловой коэффициент, т. е. тангенс угла a, образованного касательной с осью Ox . Обозначим через x 0 абсциссу точки М , а через x 1 = x 0 + D х — абсциссу точки M 1 . Угловой коэффициент секущей MM 1 равен

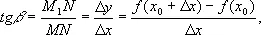
где D y = M 1N = f ( x 0 + D x ) — f ( x 0 ) — приращение функции на отрезке [ x 0 , x 1 ]. Определяя касательную в точке М как предельное положение секущей MM 1 , когда x 1 стремится к x 0 , получаем

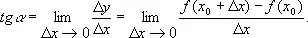
Отвлекаясь от механического или геометрического содержания приведённых задач и выделяя общий для них приём решения, приходят к понятию производной. Производной функции у = f ( x ) в точке х называется предел (если он существует) отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, так что

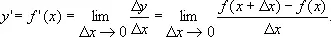
С помощью производной определяется, кроме уже рассмотренных, ряд важных понятий естествознания. Например, сила тока определяется как предел

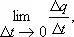
где D q — положительный электрический заряд, переносимый через сечение цепи за время D t ; скорость химической реакции определяется как предел

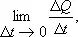
где D Q — изменение количества вещества за время D t ; вообще, производная по времени есть мера скорости процесса, применимая к самым разнообразным физическим величинам.

Производную функции y = f ( x ) обозначают f' ( x ), у' , dy/dx , df/dx или Df ( х ). Если функция y = f ( x ) имеет в точке х 0 производную, то она определена как в самой точке x 0 , так и в некоторой окрестности этой точки и непрерывна в точке x 0 . Обратное заключение было бы, однако, неверным. Например, непрерывная в каждой точке функция

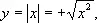
графиком которой служат биссектрисы первого и второго координатных углов, при х = 0 не имеет производной, т.к. отношение D у/ D х не имеет предела при D x ® 0: если D х > 0, это отношение равно +1, а если D x < 0, то оно равно -1. Более того, существуют непрерывные функции, не имеющие производной ни в одной точке (см. Непрерывная функция ).

Операцию нахождения производной называют дифференцированием. На классе функций, имеющих производную, эта операция линейна.

Таблица формул и правил дифференцирования

( C )´ = 0; ( x n )´ = nx n-1 ;

( a х )´ = a x ln a и ( e x )´ = e x ;

(log ax )´ = 1/ x ln a и (ln x )´ = 1/ x ;

(sin x )´ = cos x ; (cos x )´ = – sin x ;

(tg x )´ = 1/cos 2 x ; (ctg x )´ = – 1/sin 2 x ;

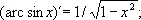
(arc tg x )´ = 1/(1 + x 2 ).

[ f ( x ) ± g ( x )]´ = f ´( x ) ± g ´( x );

[ Cf ( x )]´ = Cf ´( x );

[ f ( x ) g ( x )]´ = f ´´( x ) g ( x ) + f ( x ) g ´( x );

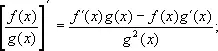
если y = f ( u ) и u = j( x ), т. е. y = f [j( x )], то dy/dx = ( dy/du )×( du/dx ) = f¢ ( u )j¢( x ).

Здесь С , n и a — постоянные, a > 0. Эта таблица, в частности, показывает, что производная от всякой элементарной функции есть снова элементарная функция.

Если производная f' ( x ), в свою очередь, имеет производную, то её называют второй производной функции у = f ( x ) и обозначают

у" , f" ( x ), d 2y/dx 2 , d 2f/dx 2 или D 2f ( x ).

Для прямолинейно движущейся точки вторая производная характеризует её ускорение.

Аналогично определяются и производные более высокого (целого) порядка. Производная порядка n обозначается

y n , f n ( x ), d ny/dx n , d nf/dx n или D nf ( x ).

Дифференциал.Функция у = f ( x ), область определения которой содержит некоторую окрестность точки х 0 , называется дифференцируемой в точке x 0 , если её приращение

D y = f ( x 0 + D x ) - f ( x 0 )

можно записать в форме

D у = А D х + aD х ,

где А = А ( x 0 ), a = a( х , x 0 ) ® 0 при х ® x 0 . В этом и только в этом случае выражение AD x называется дифференциалом функции f ( x ) в точке x 0 и обозначается dy или df ( x 0 ). Геометрически дифференциал (при фиксированном значении x 0 и меняющемся приращении D x ) изображает приращение ординаты касательной, т. е. отрезок NT (см. рис. ). Дифференциал dy представляет собой функцию как от точки х 0 , так и от приращения D х . Говорят, что дифференциал есть главная линейная часть приращения функции, понимая под этим, что, при фиксированном х 0 , dy есть линейная функция от D х и разность D y - dy есть бесконечно малая относительно D x . Для функции f ( x ) º х имеем dx = D х , т. е. дифференциал независимого переменного совпадает с его приращением. Поэтому обычно пишут dy = Adx . Имеется тесная связь между дифференциалом функции и её производной. Для того чтобы функция от одного переменного y = f (x) имела в точке x 0 дифференциал, необходимо и достаточно, чтобы она имела в этой точке (конечную) производную f' ( x 0 ), и справедливо равенство dy = f' ( x 0 ) dx . Наглядный смысл этого предложения состоит в том, что касательная к кривой y = f ( x ) в точке с абсциссой x 0 как предельное положение секущей является также такой прямой, которая в бесконечно малой окрестности точки x 0 примыкает к кривой более тесно, чем любая другая прямая. Таким образом, всегда А ( х 0 ) = f' ( x 0 ); запись dy/dx можно понимать не только как обозначение для производной f' ( x 0 ), но и как отношение дифференциалов зависимого и независимого переменных. В силу равенства dy = f' ( x 0 ) dx правила нахождения дифференциалов непосредственно вытекают из соответствующих правил нахождения производных.