БСЭ БСЭ - Большая Советская Энциклопедия (ДИ)

Следующие два простых примера могут служить иллюстрацией к сказанному.

1) Если тело, нагретое до температуры Т , помещено в среду, температура которой равна нулю, то при известных условиях можно считать, что приращение D Т (отрицательное в случае T > 0) его температуры за малый промежуток времени D t с достаточной точностью выражается формулой

D T = - kT D t ,

где k — постоянный коэффициент. При математической обработке этой физической задачи считают, что выполняется точно соответствующее предельное соотношение между дифференциалами

dT = - kTdt , (1)

т. е. имеет место Д. у.

T' = - kT ,

где T' (обозначает производную по t . Решить полученное Д. у., или, как выражаются иначе, проинтегрировать его, значит найти функции, обращающие его в тождество. Для уравнения (1) все такие функции (т. е. все его частные решения) имеют вид

Т = Ce -kt , (2)

где С постоянно. Сама формула (2) с произвольной постоянной С называется общим решением уравнения (1).

2) Пусть, например, груз р массы m подвешен к пружине и находится в положении равновесия ( рис. 1 , а). Отклоняя его от положения равновесия с помощью растяжения пружины ( рис. 1 , б), приводят груз в движение. Если x ( t ) обозначает величину отклонения тела от положения равновесия в момент времени t , то ускорение тела выражается 2-й производной x'' ( t ). Сила mх'' ( t ), действующая на тело, при небольших растяжениях пружины по законам теории упругости пропорциональна отклонению x ( t ). Т. о., получается Д. у.

mх" ( t ) = – kx ( t ). (3)

Его решение имеет вид:

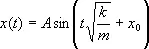
и показывает, что тело будет совершать гармонические колебания ( рис. 1 , в).

Теория Д. у. выделилась в самостоятельную детально разработанную научную дисциплину в 18 в. (труды Д. Бернулли , Ж. Д' Аламбера и особенно Л. Эйлера ).

Д. у. делятся на «обыкновенные», содержащие производные одной или нескольких функций одного независимого переменного, и «уравнения с частными производными», содержащие частные производные функций нескольких независимых переменных. Порядком Д. у. называется наибольший порядок входящих в него производных. Так, например,

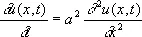
есть Д. у. с частными производными 2-го порядка.

Обыкновенные дифференциальные уравнения.Уравнения 1-го порядка. Обыкновенным Д. у. 1-го порядка с одной неизвестной функцией (только такие пока будут рассматриваться) называется соотношение

F ( x , у , у' ) = 0 (А)

между независимым переменным х , искомой функцией у и её производной

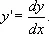
Если уравнение (А) может быть разрешено относительно производной, то получается уравнение вида

y' = f ( x , у ). (Б)

Многие вопросы теории Д. у. проще рассматривать для таких разрешённых относительно производной уравнений, предполагая функцию f ( x , y ) однозначной.

Уравнение (Б) можно записать в виде соотношения между дифференциалами

f ( x , y ) dx - dy = 0,

тогда оно становится частным случаем уравнений вида

Р ( х , у ) dx + Q ( x , у ) dy = 0. (В)

В уравнениях вида (В) естественно считать переменные х и у равноправными, т. е. не интересоваться тем, какое из них является независимым.

Геометрическая интерпретация дифференциальных уравнений. Пусть у = у ( х ) есть решение уравнения (Б). Геометрически это значит, что в прямоугольных координатах касательная к кривой у = у ( х ) имеет в каждой лежащей на ней точке М ( х , у ) угловой коэффициент k = f ( x , у ). Т. о., нахождение решений у = у ( х ) геометрически сводится к такой задаче: в каждой точке некоторой области на плоскости задано «направление», требуется найти все кривые, которые в любой своей точке М имеют направление, заранее сопоставленное этой точке. Если функция f ( x , у ) непрерывна, то это направление меняется при перемещении точки М непрерывно, и можно наглядно изобразить поле направлений, проведя в достаточно большом числе достаточно густо расположенных по всей рассматриваемой области точек короткие чёрточки с заданным для этих точек направлением. На рис. 2 это выполнено для уравнения у' = у 2 . Рисунок позволяет сразу представить себе, как должны выглядеть графики решения — так называемые интегральные кривые Д. у. Вычисление показывает, что общее решение данного уравнения есть

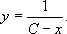
На рис. 2 вычерчены интегральные кривые, соответствующие значениям параметра С = 0 и С = 1.

График любой однозначной функции у = у ( х ) пересекает каждую прямую, параллельную оси Оу , только один раз. Таковы, следовательно, интегральные кривые любого уравнения (Б) с однозначной непрерывной функцией в правой части. Новые возможности для вида интегральных кривых открываются при переходе к уравнениям (В). При помощи пары непрерывных функций Р ( х , у ) и Q ( x , у ) можно задать любое непрерывное «поле направлений». Задача интегрирования уравнений (В) совпадает с чисто геометрической (не зависящей от выбора осей координат) задачей разыскания интегральных кривых по заданному на плоскости полю направлений. Следует заметить, что тем точкам ( x 0 , у 0 ), в которых обе функции Р ( х , у ) и Q ( x , у ) обращаются в нуль, не соответствует какое-либо определённое направление. Такие точки называются особыми точками уравнения (В).

Пусть, например, задано уравнение

ydx + xdy = 0,

которое можно записать в виде

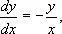
хотя, строго говоря, правая часть этого последнего уравнения теряет смысл при х = 0 и у = 0. Соответствующие поле направлений и семейство интегральных кривых, являющихся в этом случае окружностями х 2 + у 2 = С , изображены на рис. 3 . Начало координат ( х = 0, у = 0) — особая точка данного уравнения. Интегральными кривыми уравнения

ydx - xdy = 0,

изображёнными на рис. 4 , являются всевозможные прямолинейные лучи, выходящие из начала координат; начало координат является особой точкой и этого уравнения.