БСЭ БСЭ - Большая Советская Энциклопедия (ДИ)

Дифференциальные уравнения высших порядков и системы дифференциальных уравнений. Д. у. n -го порядка с одной неизвестной функцией у ( х ) независимого переменного х записывают так:

F ( х , у , y' , у" , ..., y (n-1) , y (n) ) = 0. (13)

Если ввести дополнительные неизвестные функции

y 1 = y' , y 2 = y" , ..., y n-1 = y ( n-1 ), (14)

то уравнение (13) можно заменить системой из n уравнений с n неизвестными функциями, но зато 1-го порядка. Для этого достаточно к n - 1 уравнениям (14) присоединить уравнение

F ( x , у , y 1 , у 2 , ..., y n-1 , y' n-1 ) = 0.

Аналогичным образом сводятся к системам уравнений 1-го порядка и системы уравнений высших порядков. В механике сведение систем уравнений 2-го порядка к системе из удвоенного числа уравнений 1-го порядка имеет простой механический смысл. Например, система трёх уравнений движения материальной точки

mx" = p ( x , y , z ), my" = Q ( x , у , z ),

mz" = R ( x , у , z ),

где х , у , z — координаты точки, зависящие от времени t , сводится к системе шести уравнений:

mu' = р ( х , у , z ), mv' = Q ( x , у , z ),

nw' = R ( x , у , z ), u = х' , v = y' , w = z'

при помощи введения в качестве новых переменных составляющих u , v , w скорости.

Наибольшее значение имеют системы, в которых число уравнений равно числу неизвестных функций. Система из n уравнений 1-го порядка с n неизвестными функциями, разрешённая относительно производных, имеет вид:

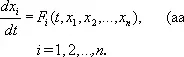
Решением системы Д. у. (а) называется система функций x 1 ( t ), x 2 ( t ), ..., x n ( t ), которая при подстановке в уравнения (а) обращает их в тождества. Часто встречаются системы вида (а), в которых правые части не зависят от t . В этом случае изучение системы (а) в основном сводится к изучению системы из ( n - 1)-го уравнения, которую целесообразно записывать в симметричной форме

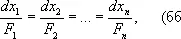
не предрешая вопроса о том, от какого из переменных х 1 , x 2 ,..., x n мыслятся зависящими остающиеся n - 1 переменных. Считая х = ( x 1 , x 2 ,..., x n ) вектором, можно записать систему (а) в виде одного векторного уравнения:

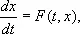
что позволяет широко пользоваться при изучении систем (а) аналогией с теорией одного уравнения 1-го порядка вида (Б). В частности, оказывается, что для систем (а) сохраняют силу основные результаты относительно существования и единственности решения задачи с начальными условиями: если в окрестности точки ( t 0 , х 1 0 , x 2 0 , ..., x n 0 ) все функции F i непрерывны по совокупности переменных t , x 1 , x 2 , ..., x n и имеют ограниченные производные по переменным x 1 , x 2 , ..., x n , то задание начальных значений x i ( t 0 ) = x i 0 , i = 1, 2, ..., n , определяет одно, вполне определённое, решение системы (а). Этим объясняется то, что, вообще говоря, решение систем из n уравнений 1-го порядка с n неизвестными функциями зависит от n параметров.

Для приведённых выше конкретных примеров Д. у. их общее решение удаётся выразить при помощи элементарных функций. Типы Д. у., допускающие такого рода решение, детально изучаются. Часто придерживаются более общей точки зрения, считая Д. у. «решённым», если искомая зависимость между переменными (и входящими в общее решение параметрами c 1 , c 2 , ...) может быть выражена при помощи элементарных функций и одной или нескольких операций взятия неопределённого интеграла («решение выражено в квадратурах»).

Большой общностью обладают способы нахождения решений при помощи разложения их в степенные ряды. Например, если правые части уравнений (а) в окрестности точки ( t 0 , x 1 0 , x 2 0 , ..., x n 0 ) голоморфны (см. Аналитические функции ), то решение соответствующей начальной задачи выражается функциями x i ( t ), разлагающимися в степенные ряды:

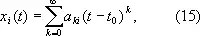
коэффициенты которых можно найти последовательным дифференцированием правых частей Д. у. (а) и сопоставлением коэффициентов при одинаковых степенях в левых и правых частях этих уравнений.

Из специальных типов Д. у. особенно хорошо разработана теория линейных Д. у. и систем линейных Д. у. (см. Линейные дифференциальные уравнения ).

Для линейных Д. у. сравнительно просто решаются также вопросы «качественного» поведения интегральных кривых, т. е. их поведение во всей области задания Д. у. Для нелинейных Д. у., где нахождение общего решения особенно сложно, вопросы качественной теории Д. у. приобретают иногда даже доминирующее значение. После классических работ А. М. Ляпунова ведущую роль в качественной теории Д. у. играют работы советских математиков, механиков и физиков. В связи с этой теорией см. Динамическая система , Особая точка , Устойчивость , Предельный цикл .

Большое значение имеет аналитическая теория Д. у., изучающая решения Д. у. с точки зрения теории аналитических функций, т. е. интересующаяся, например, расположением их особых точек в комплексной плоскости и т.п.

Наряду с рассмотренной выше начальной задачей, в которой задаются значения искомых функций (а в случае уравнений старших порядков и их производных) в одной точке (при одном значении независимого переменного), находят широкое применение краевые задачи .

Дифференциальные уравнения с частными производными.Типичной особенностью Д. у. с частными производными и систем Д. у. с частными производными является то, что для однозначного определения частного решения здесь требуется задание не значений того или иного конечного числа параметров, а некоторых функций. Например, общим решением уравнения

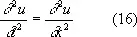
является выражение

u ( t , x ) = f ( x + t ) + g ( x - t ),

где f и g — произвольные функции. Т. о., Д. у. (16) лишь в той мере ограничивает произвол в выборе функции двух переменных u ( х , у ), что её удаётся выразить через две функции f ( z ) и g ( v ) от одного переменного, которые остаются [если в дополнение к уравнению (16) не дано каких-либо «начальных» или «краевых» условий] произвольными.