БСЭ БСЭ - Большая Советская Энциклопедия (ДИ)

Типичной задачей с начальными условиями для системы Д. у. с частными производными 1-го порядка

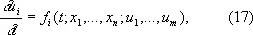
где независимыми переменными являются t , x 1,..., x n , а u 1,..., u m суть функция от этих независимых переменных, может служить задача Коши: по заданным при каком-либо t = t 0 значениям

u i ( t 0 , x 1 ,..., x n ) = j i( x 1 ,..., x n ),

i = 1, 2, ..., m ,

найти функции u i ( t , x 1 , ..., x n ).

В теории Д. у. с частными производными порядка выше первого и систем Д. у. с частными производными рассматриваются как задачи типа Коши, так и ряд краевых задач.

При постановке и решении краевых задач для Д. у. с частными производными порядка выше первого существенное значение имеет тип уравнения. В качестве примера можно привести классификацию Д. у. с частными производными 2-го порядка с одной неизвестной функцией z ( х , у ) от двух переменных:

F ( x , у , z , р , q , r , s , t ) = 0, (18)

где

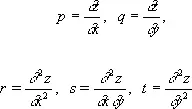
Если

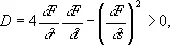
то (18) есть эллиптическое уравнение. Примером может служить уравнение Лапласа:

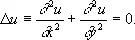
Если D < 0, то (18) есть гиперболическое уравнение. Примером может служить уравнение колебания струны:

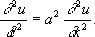
Если D = 0, то (18) есть параболическое уравнение. Примером может служить уравнение распространения тепла:

О краевых задачах для этих различных типов уравнений см. Уравнения математической физики .

Лит.: Обыкновенные Д. у.Степанов В. В., Курс дифференциальных уравнений, 8 изд., М., 1959; Петровский И. Г., Лекции по теории обыкновенных дифференциальных уравнений, 5 изд., М., 1964; Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 2 изд., М., 1965; Камке Э., Справочник по обыкновенным дифференциальным уравнениям, пер. с нем., 3 изд., М., 1965; Филиппов А. Ф., Сборник задач по дифференциальным уравнениям, 2 изд., М., 1965.

Д. у. с частными производными.Петровский И. Г., Лекции об уравнениях с частными производными, 3 изд., М., 1961; Тихонов А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М., 1966; Соболев С. Л., Уравнения математической физики, 4 изд., М., 1966; Смирнов М. М., Задачи по уравнениям математической физики, 5 изд., М., 1968.

По материалам одноимённой статьи из 2-го издания БСЭ.

Рис. 8 к ст. Дифференциальные уравнения.

Рис. 1 к ст. Дифференциальные уравнения.

Рис. 3 к ст. Дифференциальные уравнения.

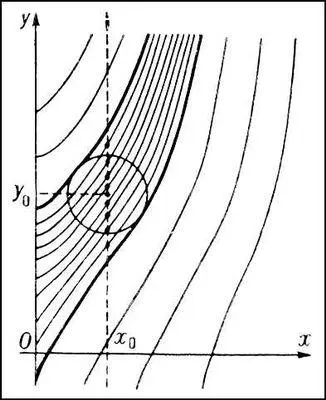
Рис. 6 к ст. Дифференциальные уравнения.

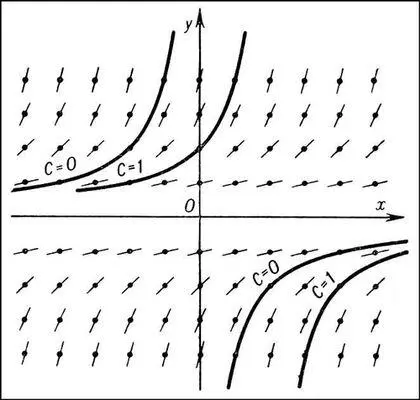
Рис. 2 к ст. Дифференциальные уравнения.

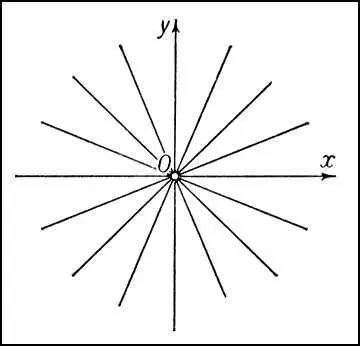
Рис. 4 к ст. Дифференциальные уравнения.

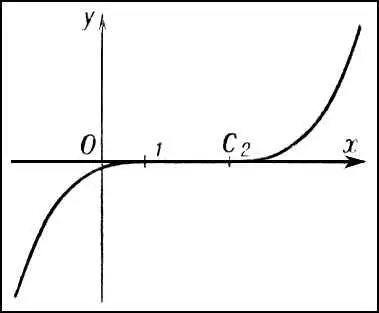
Рис. 7 к ст. Дифференциальные уравнения.

Рис. 5 к ст. Дифференциальные уравнения.

«Дифференциа'льные уравне'ния»,ежемесячный научный математический журнал, основан в 1965, издаётся в Минске. Публикует результаты исследований в области дифференциальных, интегро-дифференциальных и интегральных уравнений, а также уравнений в конечных разностях. Переводится в США на английский язык и издается под названием «Differential equations».

Дифференциа'льные уравне'ния с отклоня'ющимся аргуме'нтом,уравнения, связывающие аргумент, а также искомую функцию и её производные, взятые, вообще говоря, при различных значениях этого аргумента (в отличие от обычных дифференциальных уравнений ). Примерами могут служить уравнения

x’' ( t ) = ax ( t - t) (1)

и

x’' ( t ) = ax ( kt ), (2)

где постоянные а , t, k заданы; t = t - ( t - t) в уравнении (1) и t - kt в уравнении (2) — отклонения аргумента. Такие уравнения появились в конце 18 в. Неоднократно рассматривались сами по себе и в связи с решением геометрических задач, а позднее — в связи с различными приложениями, прежде всего к теории регулирования. Построение систематической теории Д. у. с о. а. было начато в 50-х гг. 20 в., а уже с 60-х гг. эта теория представляет собой значительный отдел математического анализа.

Наиболее хорошо изучены линейные однородные автономные (т. е. с постоянными коэффициентами и постоянными отклонениями аргумента) Д. у. с о. а.; к таким уравнениям относится, например, (1). Здесь имеется достаточно полная система решений вида х = e рt , причём для отыскания р получается трансцендентное характеристическое уравнение вида Р ( р ) = 0, где Р ( р ) — сумма членов вида Ap m е a p , m ³ 0 — целое [например, для (1) имеем Р ( р ) º р - ае - t p ]. Это уравнение имеет, вообще говоря, бесконечное число комплексных корней. Прочие решения рассматриваемого Д. у. с о. а. разлагаются в ряды по указанным простейшим решениям, и поэтому об основных свойствах совокупности решений, в частности об их устойчивости, можно судить по расположению нулей функции Р ( р ).

Важнейший и наиболее изученный класс Д. у. с о. а. образуют дифференциальные уравнения с запаздывающим аргументом, в которых старшая производная от искомой функции при каком-либо значении аргумента определяется через саму эту функцию и её младшие производные, взятые при меньших либо равных значениях аргумента. Примеры: уравнение (1) при t ³ 0 (t—запаздывание); уравнение (2) при k £ 1 и t ³ 0. Эти уравнения и их системы, если аргументом служит время, описывают процессы с последействием, скорость которых в любой момент определяется их состоянием не только в тот же момент (как для обычных дифференциальных уравнении), но и в предшествующие моменты. Такая ситуация возникает, в частности, в системах автоматического управления при наличии запаздывания в органе управления. Уравнения с запаздывающим аргументом во многом напоминают обыкновенные дифференциальные уравнения, однако в ряде отношений отличаются от них. Например, если решение уравнения (1) строится при t ³ t 0 , то в качестве начального условия х ( t ) должно быть задано при t 0 - t £ t £ t 0 ; решение можно строить последовательно на интервалах t 0 £ t £ t 0 + t, t 0 + t £ t 0 + 2t, пользуясь на каждом шаге результатом вычислений с предыдущего шага. В линейном автономном случае к таким уравнениям можно применять методы операционного исчисления .