БСЭ БСЭ - Большая Советская Энциклопедия (ДИ)

Начальные условия. Геометрическая интерпретация Д. у. 1-го порядка приводит к мысли, что через каждую внутреннюю точку М области G с заданным непрерывным полем направлений можно провести одну вполне определённую интегральную кривую.

В отношении существования интегральной кривой сформулированная гипотеза оказывается правильной. Доказательство этого предложения принадлежит Дж. Пеано . В отношении же единственности интегральной кривой, проходящей через заданную точку, высказанная выше гипотеза оказывается, вообще говоря, ошибочной. Уже для такого простого уравнения, как

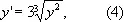
у которого правая часть непрерывна во всей плоскости, интегральные кривые имеют вид, изображённый на рис. 5 . Единственность интегральной кривой, проходящей через заданную точку, нарушается здесь во всех точках оси Ox .

Единственность, т. е. однозначное определение интегральной кривой условием её прохождения через заданную точку, имеет место для уравнений (Б) с непрерывной правой частью при том дополнительном условии, что функция f ( х , у ) имеет в рассматриваемой области ограниченную производную по у .

Это требование является частным случаем следующего, несколько более широкого условия Липшица: существует такая постоянная L , что в рассматриваемой области всегда

| f ( x , y 1 ) - f ( x , y 2 )| < L | у 1 – у 2 |.

Это условие чаще всего приводится в учебниках как достаточное условие единственности.

С аналитической стороны теоремы существования и единственности для уравнения вида (Б) обозначают следующее: если выполнены надлежащие условия [например, функция f ( x , y ) непрерывна и имеет ограниченную производную по у ], то задание для «начального» значения x 0 независимого переменного х «начального» значения у 0 = у ( x 0 ) функции у ( х ) выделяет из семейства всех решений у ( х ) одно определённое решение. Например, если для рассмотренного выше уравнения (1) потребовать, чтобы в начальный момент времени t 0 = 0 температура тела была равна «начальному» значению Т 0 , то из бесконечного семейства решений (2) выделится одно определённое решение, удовлетворяющее заданным начальным условиям:

T ( t ) = T 0e -kt .

Этот пример типичен: в механике и физике Д. у. обычно определяют общие законы течения какого-либо явления; однако, чтобы получить из этих законов определённые количественные результаты, надо присоединить к ним сведения о начальном состоянии изучаемой физической системы в некоторый определённый выбранный в качестве «начального» момент времени t 0 .

Если условия единственности выполнены, то решение y ( x ), удовлетворяющее условию у ( x 0 ) = у 0 , можно записать в виде:

y ( x ) = j( x ; х 0 , у 0 ), (5)

где x 0 и у 0 входят как параметры, функция же j ( х ; x 0 , y 0 ) трёх переменных х , x 0 и y 0 однозначно определяется самим уравнением (Б). Важно отметить, что при достаточно малом изменении поля (правой части Д. у.) функция j( х ; x 0 , у 0 ) меняется сколь угодно мало на конечном промежутке изменения переменного х — имеется непрерывная зависимость решения от правой части Д. у. Если правая часть f ( x , у ) Д. у. непрерывна и её производная по у ограничена (или удовлетворяет условию Липшица), то имеет место также непрерывность j( х ; х 0 , у 0 ) по x 0 и y 0 .

Если в окрестности точки ( х 0 , у 0 ) для уравнения (Б) выполнены условия единственности, то все интегральные кривые, проходящие через достаточно малую окрестность точки ( x 0 , у 0 ), пересекают вертикальную прямую х = х 0 и определяются ординатой у = С своей точки пересечения с этой прямой (см. рис. 6 ). Т. о., все эти решения содержатся в семействе с одним параметром С :

y ( x ) = F ( x , C ),

которое является общим решением Д. у. (Б).

В окрестности точек, в которых нарушаются условия единственности, картина может быть сложнее. Весьма сложен и вопрос о поведении интегральных кривых «в целом», а не в окрестности точки ( x 0 , у 0 ).

Общий интеграл. Особые решения. Естественно поставить обратную задачу: задано семейство кривых, зависящих от параметра С, требуется найти Д. у., для которого кривые заданного семейства служили бы интегральными кривыми. Общий метод для решения этой задачи заключается в следующем: считая семейство кривых на плоскости хОу заданным при помощи соотношения

F ( x , y , C ) = 0, (6)

дифференцируют (6) при постоянном С и получают

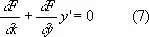
или в симметричной записи

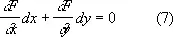
и из двух уравнений (6) и (7) или (6) и (8) исключают параметр С . Если данное Д. у. получается таким образом из соотношения (6), то это соотношение называется общим интегралом заданного Д. у. Одно и то же Д. у. может иметь много различных общих интегралов. После нахождения для заданного Д. у. общего интеграла оказывается необходимым, вообще говоря, ещё исследовать, не имеет ли Д. у. дополнительных решений, не содержащихся в семействе интегральных кривых (6).

Пусть, например, задано семейство кривых

( х - С ) 3- у = 0. (9)

Дифференцируя (9) при постоянном С получают

3( х - С ) 2- у' = 0,

после же исключения С приходят к Д. у.

27 y 2 - ( y ') 3= 0, (10)

равносильному уравнению (4). Легко видеть, что кроме решений (9), уравнение (10) имеет решение

y º 0. (11)

Решение уравнения (10) самого общего вида таково:

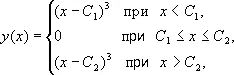
где -¥ £ C 1£ C 2£ +¥ ( рис. 7 ). Оно зависит от двух параметров C 1и C 2, но составляется из кусков кривых однопараметрического семейства (9) и куска особого решения (11).

Решение (11) уравнения (10) может служить примером особого решения Д. у. В качестве другого примера можно рассмотреть семейство прямых

4( у - Cx ) + C 2 = 0. (12)

Эти прямые являются интегральными кривыми Д. у.

4( у - ху' ) + ( у' ) 2= 0.

Особой же интегральной кривой этого Д. у. служит парабола

х 2 - у = 0,

огибающая прямые (12) ( рис. 8 ). Картина, наблюдавшаяся в рассмотренном примере, типична; особые интегральные кривые обычно являются огибающими семейства интегральных кривых, получаемых из общего решения.