БСЭ БСЭ - Большая Советская Энциклопедия (ДИ)

Д. р. II возникает в результате различной производительности добавочных вложений: её масса и норма планомерно возрастают в условиях интенсификации, научно-технического прогресса в с.-х. производстве; она почти полностью остаётся у с.-х. предприятий.

Сложившиеся в социалистических странах различные отношения земельной собственности обусловливают и разные конкретные формы распределения Д. р. Однако сущность рентных отношений и общие принципы распределения Д. р. остаются едиными независимо от того, вся земля национализирована или часть её находится в собственности кооперативов. В правильном экономическом регулировании рентных отношений при социализме важное значение имеет эффективное применение механизма распределения Д. р., прежде всего научно обоснованное ценообразование, учитывающее специфику сельского хозяйства.

Д. р. существует не только в сельском хозяйстве, но и в добывающей промышленности, строительстве, образуется в результате различий в производительности труда, обусловленных неравенством естественных условий разработки и использования полезных ископаемых, лесных угодий и т.д. При социализме Д. р. в добывающей промышленности принадлежит всему обществу и используется в его интересах, в том числе для развития угольной, рудной и др. отраслей. Как стоимостная категория Д. р. перестанет существовать с отмиранием товарного производства.

Лит . см. при ст. Земельная рента .

И. Н. Буздалов.

Дифференциа'льно-диагности'ческие сре'ды,специальные смеси питательных веществ (см. Питательные среды ), на которых выращивают микроорганизмы для определения их видовой принадлежности. К Д.-д. с. относятся белковые среды, применяемые для определения гемолитической и протеолитической способности микробов; среды, содержащие углеводы и индикаторы изменения кислотности (в результате утилизации микробами этих соединений); среды, содержащие вещества, служащие источником питания только для определённых видов бактерий, и др.

Дифференциа'льное исчисле'ние,раздел математики, в котором изучаются производные и дифференциалы функций и их применения к исследованию функций. Оформление Д. и. в самостоятельную математическую дисциплину связано с именами И. Ньютона и Г. Лейбница (вторая половина 17 в.). Они сформулировали основные положения Д. и. и чётко указали на взаимно обратный характер операций дифференцирования и интегрирования. С этого времени Д. и. развивается в тесной связи с интегральным исчислением , вместе с которым оно составляет основную часть математического анализа (или анализа бесконечно малых). Создание дифференциального и интегрального исчислений открыло новую эпоху в развитии математики. Оно повлекло за собой появление ряда математических дисциплин: теории рядов, теории дифференциальных уравнений, дифференциальной геометрии и вариационного исчисления. Методы математического анализа нашли применение во всех разделах математики. Неизмеримо расширилась область приложений математики к вопросам естествознания и техники. «Лишь дифференциальное исчисление дает естествознанию возможность изображать математически не только состояния, но и процессы: движение» (Энгельс Ф., см. Маркс К. и Энгельс Ф., Соч., 2 изд., т. 20, с. 587).

Д. и. зиждется на следующих важнейших понятиях математики, определение и исследование которых составляют предмет введения в математический анализ: действительные числа (числовая прямая), функция , предел , непрерывность . Все эти понятия выкристаллизовались и получили современное содержание в ходе развития и обоснования дифференциального и интегрального исчислений. Основная идея Д. и. состоит в изучении функций в малом. Точнее: Д. и. даёт аппарат для исследования функций, поведение которых в достаточно малой окрестности каждой точки близко к поведению линейной функции или многочлена. Таким аппаратом служат центральные понятия Д. и.: производная и дифференциал. Понятие производной возникло из большого числа задач естествознания и математики, приводящихся к вычислению пределов одного и того же типа. Важнейшие из них — определение скорости прямолинейного движения точки и построение касательной к кривой. Понятие дифференциала является математическим выражением близости функции к линейной в малой окрестности исследуемой точки. В отличие от производной, оно легко переносится на отображения одного евклидова пространства в другое и на отображения произвольных линейных нормированных пространств и является одним из основных понятий современного нелинейного функционального анализа .

Производная.Пусть требуется определить скорость прямолинейно движущейся материальной точки. Если движение равномерно, то пройденный точкой путь пропорционален времени движения; скорость такого движения можно определить как путь, пройденный за единицу времени, или как отношение пути, пройденного за некоторый промежуток времени, к длительности этого промежутка. Если же движение неравномерно, то пути, пройденные точкой в одинаковые по длительности промежутки времени, будут, вообще говоря, различными. Пример неравномерного движения даёт тело, свободно падающее в пустоте. Закон движения такого тела выражается формулой s = gt 2 /2, где s — пройденный путь с начала падения (в метрах), t — время падения (в секундах), g — постоянная величина, ускорение свободного падения, g » 9,81 м/сек 2 . За первую секунду падения тело пройдёт около 4,9 м , за вторую — около 14,7 м , а за десятую — около 93,2 м , т. е. падение происходит неравномерно. Поэтому приведённое выше определение скорости здесь неприемлемо. В этом случае рассматривается средняя скорость движения за некоторый промежуток времени после (или до) фиксированного момента t ; она определяется как отношение длины пути, пройденного за этот промежуток времени, к его длительности. Эта средняя скорость зависит не только от момента t , но и от выбора промежутка времени. В нашем примере средняя скорость падения за промежуток времени от t до t + D t равна

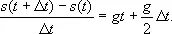
Это выражение при неограниченном уменьшении промежутка времени D t приближается к величине gt , которую называют скоростью движения в момент времени t . Таким образом, скорость движения в какой-либо момент времени определяется как предел средней скорости, когда промежуток времени неограниченно уменьшается.