БСЭ БСЭ - Большая Советская Энциклопедия (КА)

По значению для составления той или иной конкретной карты К. и. условно делятся на: основные, с которых заимствуется основное содержание карты; дополнительные, служащие для уточнения отдельных элементов; вспомогательные, привлекаемые для общей ориентировки, ознакомления с картографируемой территорией, а также с типами карт и атласов, сходными с проектируемыми или составляемыми.

При оценке К. и. используют разнообразные критерии. Например, при оценке качества астрономо-геодезических источников учитываются их точность и единство исходных данных с системой координат, используемой на составляемой карте; при определении пригодности фотоснимков — их стереофотограмметрического и фотографического качества, современность. Основными критериями при оценке общегеографических карт являются их масштаб, целевое назначение, авторство, геометрическая точность, современность, полнота содержания и качество картографической генерализации, технико-экономическая целесообразность использования источника. Важным, а в ряде случаев важнейшим критерием оценки общегеографических и многих тематических карт является их идейно-политическая направленность. Изучение и анализ текстовых и табличных источников относятся к специальным разделам картографии (картографии населения, экономической, исторической, почвенной картографии и др.).

Лит.: Бюшгенс Л. М., Анализ и оценка иностранных общегеографическнх карт как материалов для составления, М., 1957; Салищев К. А., Основы картоведения, 3 изд., т. 2, М., 1962.

Л. М. Бюшгенс.

Картографи'ческие прибо'ры,приборы, применяемые при составлении и оформлении (подготовке к изданию) карт. При составлении математической основы (картографической сетки и опорных пунктов) применяются координатографы , штангенциркули с линейками ЛБЛ, лекала, линейки Дробышева (для прочерчивания дуг окружностей с помощью отверстий со скошенными краями), нормальные (женевские) линейки (для измерения линий с точностью до 0,2 мм с помощью 2 передвижных луп). При перенесении картографического изображения с источника на составляемую карту используются приборы, позволяющие уменьшать или увеличивать изображение без изменения картографической проекции источника ( пантографы , репродукционные установки, проекторы), а также осуществлять преобразование картографической проекции исходного материала ( картографические трансформаторы ). При подготовке составительских и оформительских (издательских) оригиналов карт используют чертёжные и гравировальные инструменты. См. также Картоиздательские процессы , Картосоставительские процессы .

А. Г. Иванов.

Картографи'ческие прое'кции,отображения всей поверхности земного эллипсоида или какую-либо её части на плоскость, получаемые в основном с целью построения карты.

Масштаб.К. п. строятся в определённом масштабе. Уменьшая мысленно земной эллипсоид в М раз, например в 10 000 000 раз, получают его геометрическую модель — глобус , изображение которого уже в натуральную величину на плоскости даёт карту поверхности этого эллипсоида. Величина 1: М (в примере 1: 10 000 000) определяет главный, или общий, масштаб карты. Т. к. поверхности эллипсоида и шара не могут быть развёрнуты на плоскость без разрывов и складок (они не принадлежат к классу развёртывающихся поверхностей ), любой К. п. присущи искажения длин линий, углов и т.п., свойственные всякой карте. Основной характеристикой К. п. в любой её точке является частный масштаб m. Это — величина, обратная отношению бесконечно малого отрезка ds на земном эллипсоиде к его изображению ds на плоскости: 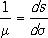причем m зависит от положения точки на эллипсоиде и от направления выбранного отрезка. Ясно, что m min£ m £ m max , и равенство здесь возможно лишь в отдельных точках или вдоль некоторых линий на карте. Т. о., главный масштаб карты характеризует её только в общих чертах, в некотором осреднённом виде. Отношение m/М называют относительным масштабом, или увеличением длины, разность 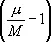искажением длины. При анализе свойств К. п. можно не принимать во внимание главный масштаб; численное значение его учитывается только при вычислениях координат точек К. п. Поэтому часто, например в теории искажений, считают М = 1.

Общие сведения.Теория К. п. — математическая картография— имеет своей целью изучение всех видов искажений отображений поверхности земного эллипсоида на плоскость и разработку методов построения таких проекций, в которых искажения имели бы или наименьшие (в каком-либо смысле) значения или заранее заданное распределение.

Исходя из нужд картографии , в теории К. п. рассматривают отображения поверхности земного эллипсоида на плоскость. Т. к. земной эллипсоид имеет малое сжатие, и его поверхность незначительно отступает от сферы, а также в связи с тем, что К. п. необходимы для составления карт в средних и мелких масштабах ( М > 1 000 000), то часто ограничиваются рассмотрением отображений на плоскость сферы некоторого радиуса R , отклонениями которой от эллипсоида можно пренебречь или каким-либо способом учесть. Поэтому далее имеются в виду отображения на плоскость хОу сферы, отнесённой к географическим координатам j (широта) и l (долгота).

Уравнения любой К. п. имеют вид

x = f 1(j, l), y = f 2(j, l) , (1)

где f 1и f 2— функции, удовлетворяющие некоторым общим условиям. Изображения меридианов l = const и параллелей j = const в данной К. п. образуют картографическую сетку. К. п. может быть определена также двумя уравнениями, в которых фигурируют не прямоугольные координаты х , у плоскости, а какие-либо иные. Некоторые К. п. [например, перспективные проекции (в частности, ортографические, рис. 2 ) перспективно-цилиндрические ( рис. 7 ) и др.] можно определить геометрическими построениями. К. п. определяют также правилом построения соответствующей ей картографической сетки или такими её характеристическими свойствами, из которых могут быть получены уравнения вида (1), полностью определяющие проекцию.

Краткие исторические сведения.Развитие теории К. п., как и всей картографии, тесно связано с развитием геодезии, астрономии, географии, математики. Научные основы картографии были заложены в Древней Греции (6—1 вв. до н. э.). Древнейшей К. п. считается гномоническая проекция , примененная Фалесом Милетским к построению карт звёздного неба. После установления в 3 в. до н. э. шарообразности Земли К. п. стали изобретаться и использоваться при составлении географических карт ( Гиппарх , Птолемей и др.). Значительный подъём картографии в 16 в., вызванный Великими географическими открытиями, привёл к созданию ряда новых проекций; одна из них, предложенная Г. Меркатором , используется и в настоящее время (см. Меркатора проекция ). В 17—18 вв., когда широкая организация топографических съёмок стала поставлять достоверный материал для составления карт на значительной территории, К. п. разрабатывались как основа для топографических карт (французский картограф Р. Бонн, Дж. Д. Кассини ), а также выполнялись исследования отдельных наиболее важных групп К. п. (И. Ламберт , Л. Эйлер , Ж. Лагранж и др.). Развитие военной картографии и дальнейшее увеличение объёма топографических работ в 19 в. потребовали обеспечения математической основы крупномасштабных карт и введения системы прямоугольных координат на базе, более подходящей К. п. Это привело К. Гаусса к разработке фундаментальной геодезической проекции . Наконец, в середине 19 в. А. Тиссо (Франция) дал общую теорию искажений К. п. Развитие теории К. п. в России было тесно связано с запросами практики и дало много оригинальных результатов (Л. Эйлер, Ф. И. Шуберт , П. Л. Чебышев , Д. А. Граве и др.). В трудах советских картографов В. В. Каврайского , Н. А. Урмаева и др. разработаны новые группы К. и., отдельные их варианты (до стадии практического использования), важные вопросы общей теории К. п., классификации их и др.