БСЭ БСЭ - Большая Советская Энциклопедия (КА)

Существует много проекций, не относящихся к указанным видам. Цилиндрические, конические и азимутальные проекции, называемые простейшими, часто относят к круговым проекциям в широком смысле, выделяя из них круговые проекции в узком смысле — проекции, в которых все меридианы и параллели изображаются окружностями, например конформные проекции Лагранжа, проекция Гринтена и др.

Использование и выбор картографических проекцийзависят главным образом от назначения карты и её масштаба, которыми часто обусловливается характер допускаемых искажений в избираемой К. п. Карты крупных и средних масштабов, предназначенные для решения метрических задач, обычно составляют в равноугольных проекциях, а карты мелких масштабов, используемые для общих обозрений и определения соотношения площадей каких-либо территорий — в равновеликих. При этом возможно некоторое нарушение определяющих условий этих проекций ( w º 0 или р º 1 ), не приводящее к ощутимым погрешностям, т. е. допустим выбор произвольных проекций, из которых чаще применяют проекции равнопромежуточные по меридианам. К последним прибегают и тогда, когда назначением карты вообще не предусмотрено сохранение углов или площадей. При выборе К. п. начинают с простейших, затем переходят к более сложным проекциям, даже, возможно, модифицируя их. Если ни одна из известных К. п. не удовлетворяет требованиям, предъявляемым к составляемой карте со стороны её назначения, то изыскивают новую, наиболее подходящую К. п., пытаясь (насколько это возможно) уменьшить искажения в ней. Проблема построения наивыгоднейших К. п., в которых искажения в каком-либо смысле сведены до минимума, полностью ещё не решена.

К. п. используются также в навигации, астрономии, кристаллографии и др.; их изыскивают для целей картографирования Луны, планет и др. небесных тел.

Преобразование проекций.Рассматривая две К. п., заданные соответствующими системами уравнений: x = f 1(j, l) , y = f 2(j, l) и X = g 1(j, l) , Y = g 2(j, l) , можно, исключая из этих уравнении j и l, установить переход от одной из них к другой:

Х = F 1(x, у) , Y = F 2(x, у) .

Эти формулы при конкретизации вида функций F 1, F 2, во-первых, дают общий метод получения так называемых производных проекций; во-вторых, составляют теоретическую основу всевозможных способов технических приёмов составления карт (см. Географические карты ). Например, аффинные и дробно-линейные преобразования осуществляются при помощи картографических трансформаторов . Однако более общие преобразования требуют применения новой, в частности электронной, техники. Задача создания совершенных трансформаторов К. п. — актуальная проблема современной картографии.

Лит.: Витковский В., Картография. (Теория картографических проекций), СПБ. 1907; Каврайский В. В., Математическая картография, М. — Л., 1934; его же, Избр. труды, т. 2, в. 1—3, [М.], 1958—60; Урмаев Н. А., Математическая картография, М., 1941; его же, Методы изыскания новых картографических проекций, М., 1947; Граур А. В., Математическая картография, 2 изд., Л., 1956; Гинзбург Г. А., Картографические проекции, М., 1951; Мещеряков Г. А., Теоретические основы математической картографии, М., 1968.

Г. А. Мещеряков.

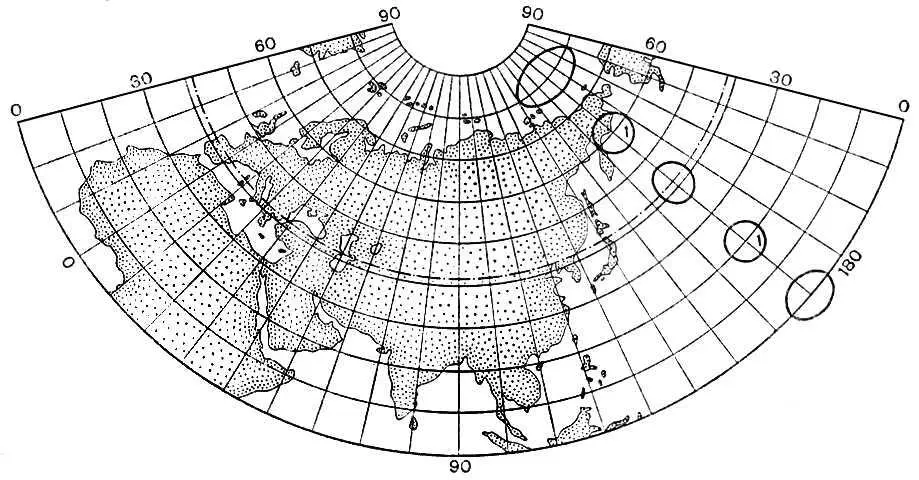
4б. Конические проекции. Равнопромежуточная.

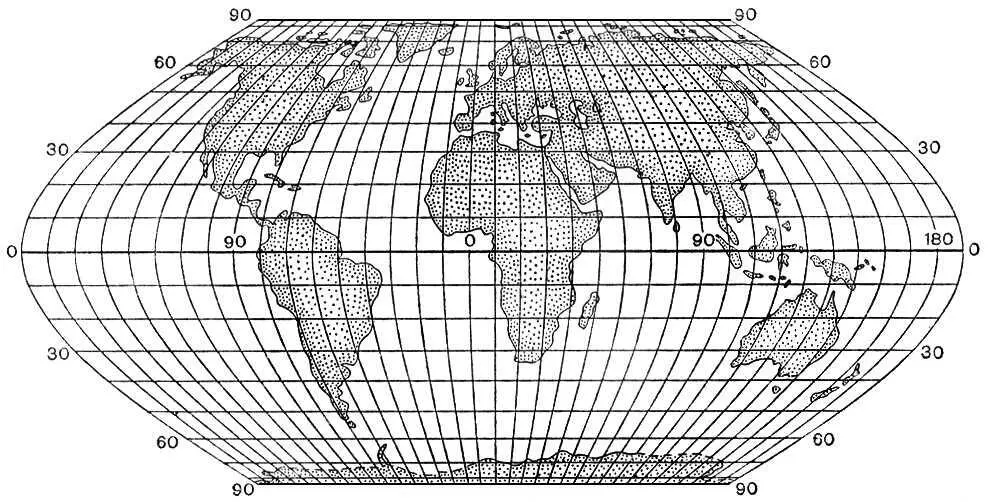
Рис. 8б. Псевдоцилиндрические проекции. Равновеликая синусоидальная проекция В. В. Каврайского.

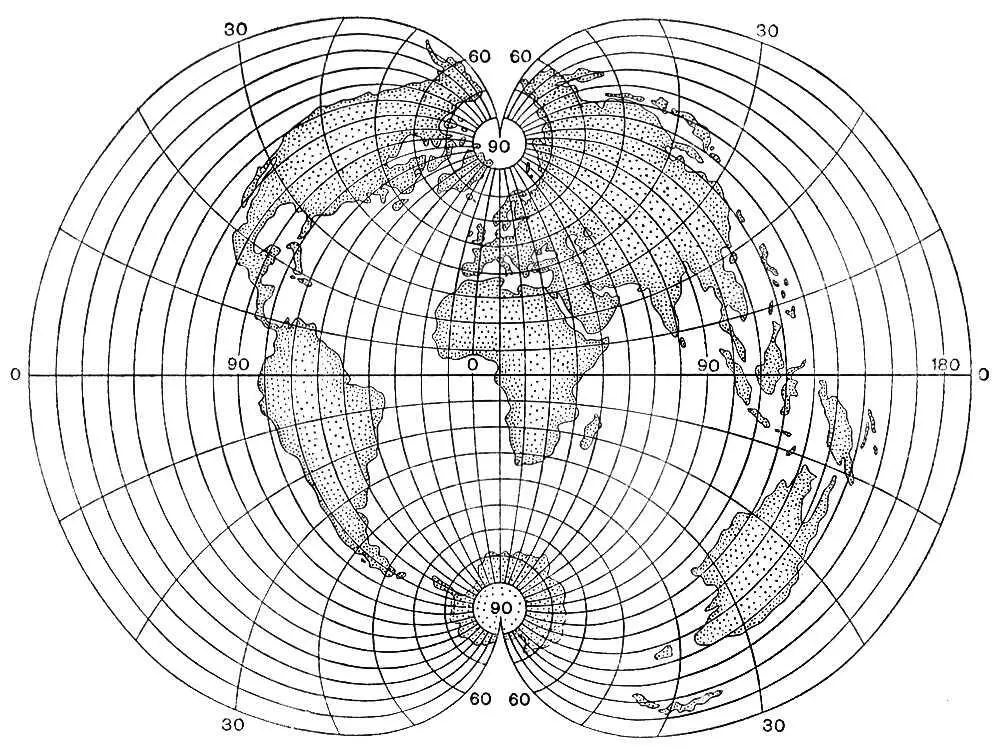
Рис. 9а. Поликонические проекции. Простая.

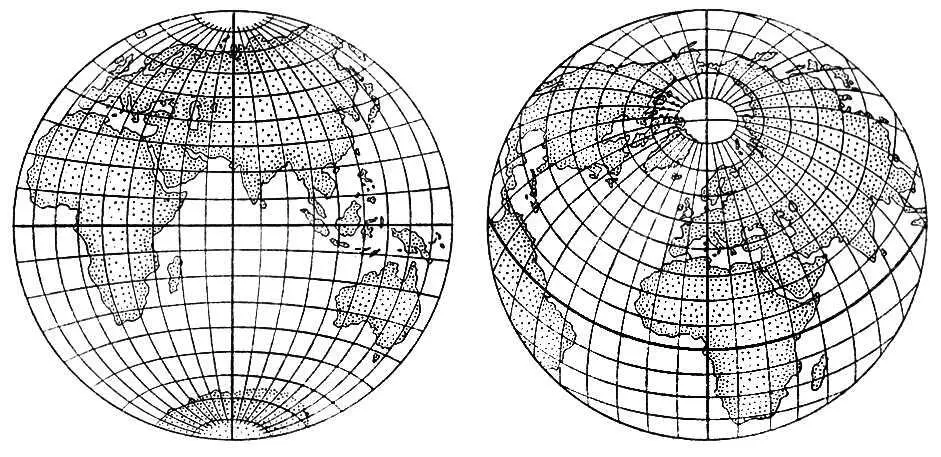
Рис. 5в. Азимутальные проекции. Равновеликая (слева — поперечная, справа — косая).

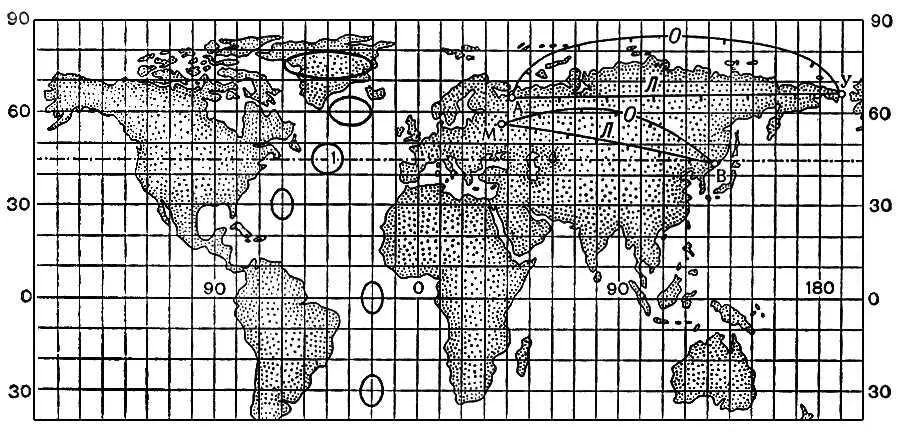
3б. Цилиндрические проекции. Равнопромежуточная (прямоугольная).

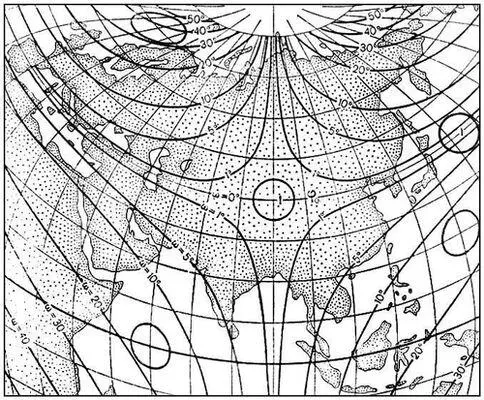
Рис. 6. Псевдоконическая равновеликая проекция Бонна.

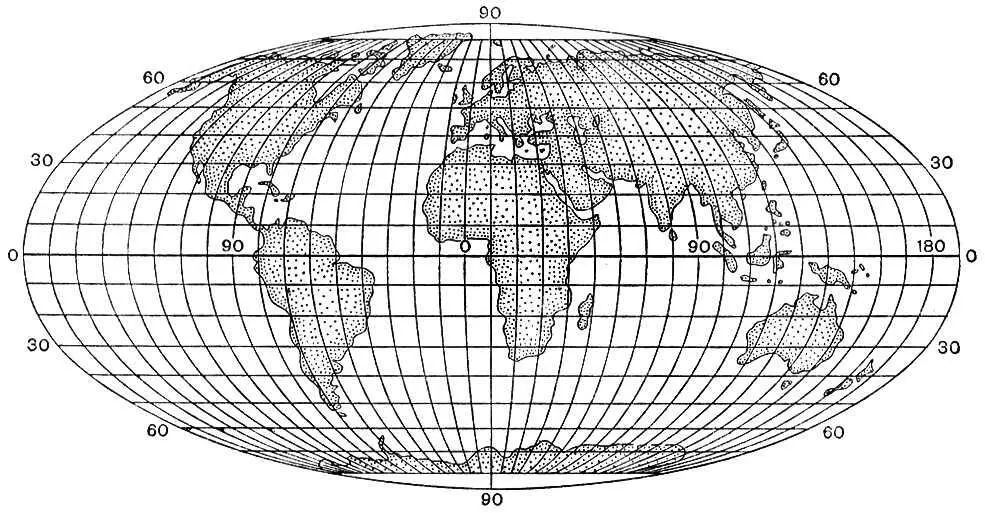
Рис. 8а. Псевдоцилиндрические проекции. Равновеликая проекция Мольвейде.

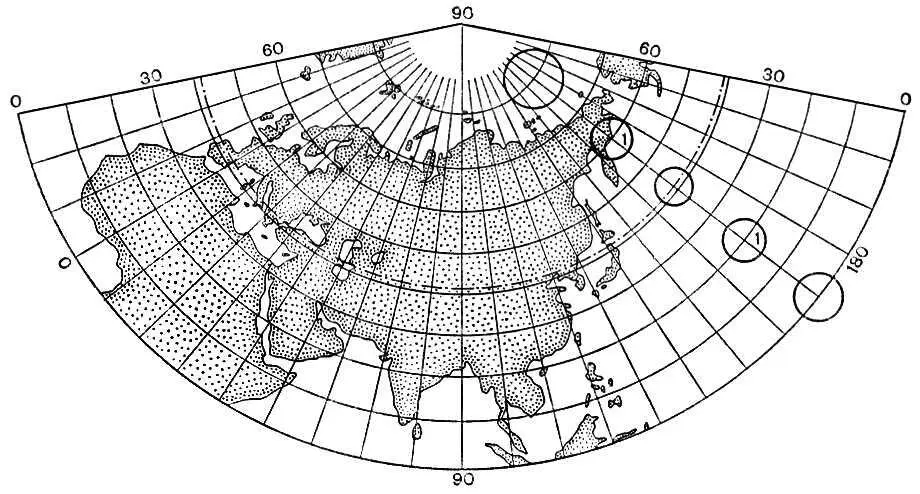
4а. Конические проекции. Равноугольная.

Рис. 5б. Азимутальные проекции. Равнопромежуточная (слева — поперечная, справа — косая).

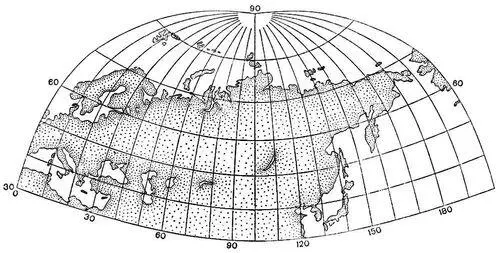
Рис. 7. Косая перспективно-цилиндрическая проекция М. Д. Соловьёва.

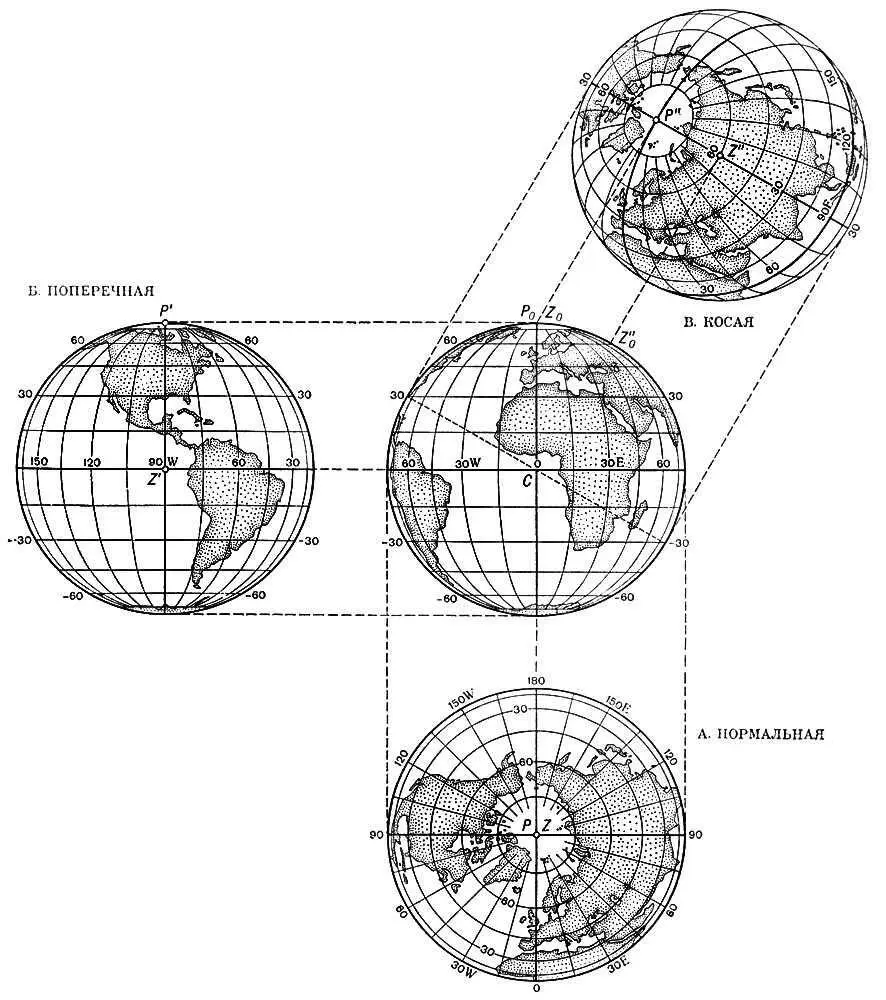
2. Шар и его ортографические проекции.

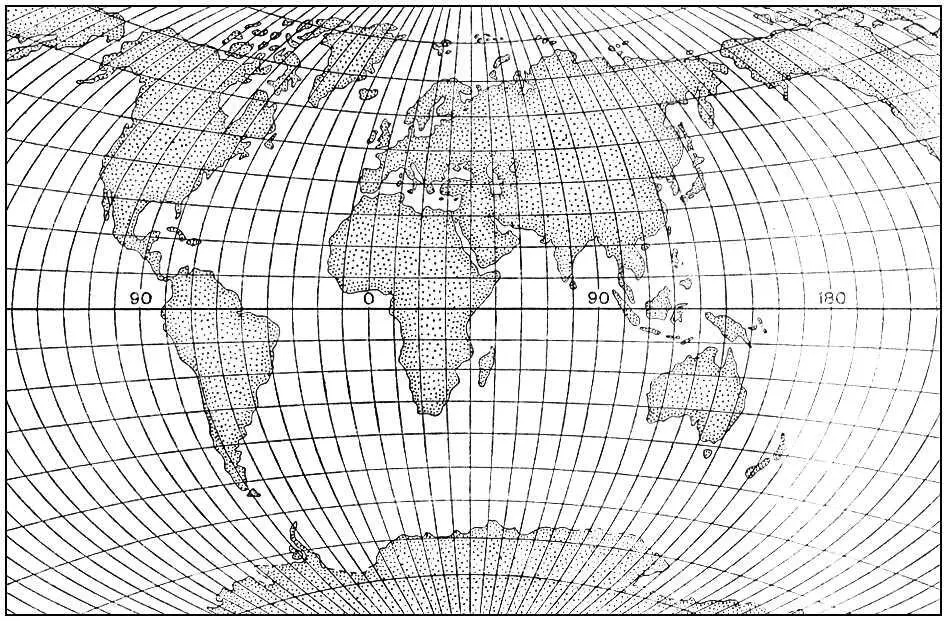
Рис. 9б. Поликонические проекции. Произвольная проекция Г. А. Гинзбурга.

4в. Конические проекции. Равновеликая.

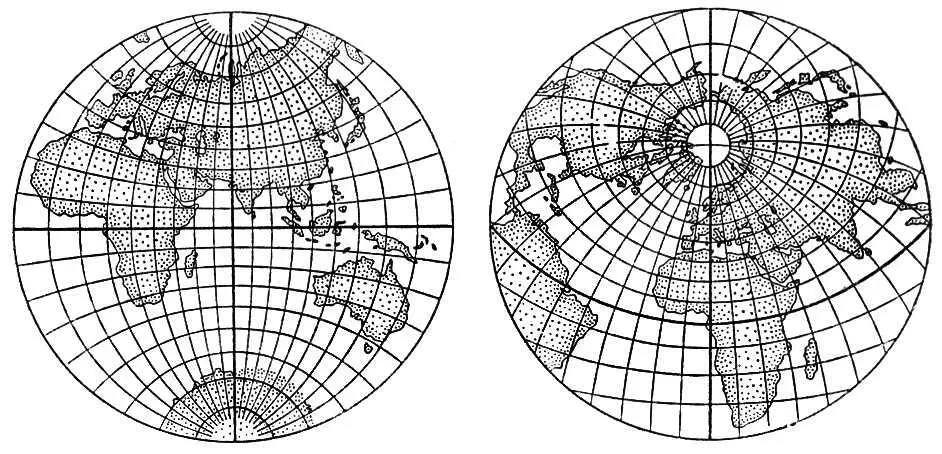
Рис. 5а. Азимутальные проекции. Равноугольная (стереографическая) слева — поперечная, справа — косая.

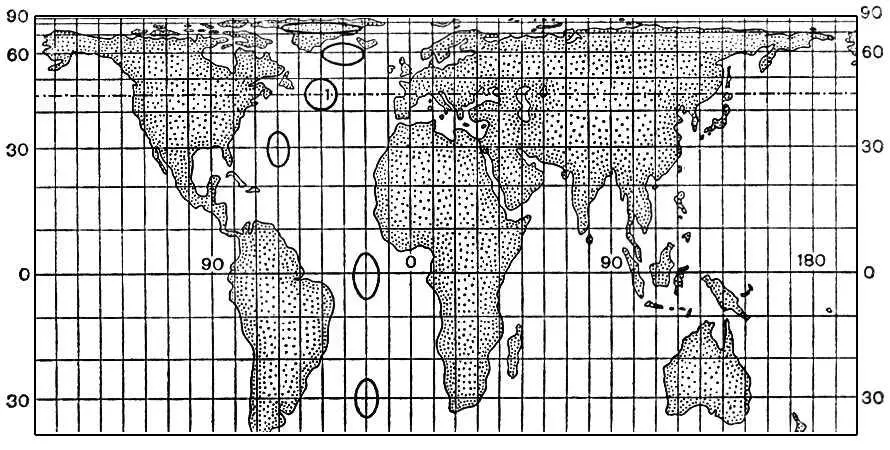
3в. Цилиндрические проекции. Равновеликая (изоцилиндрическая).

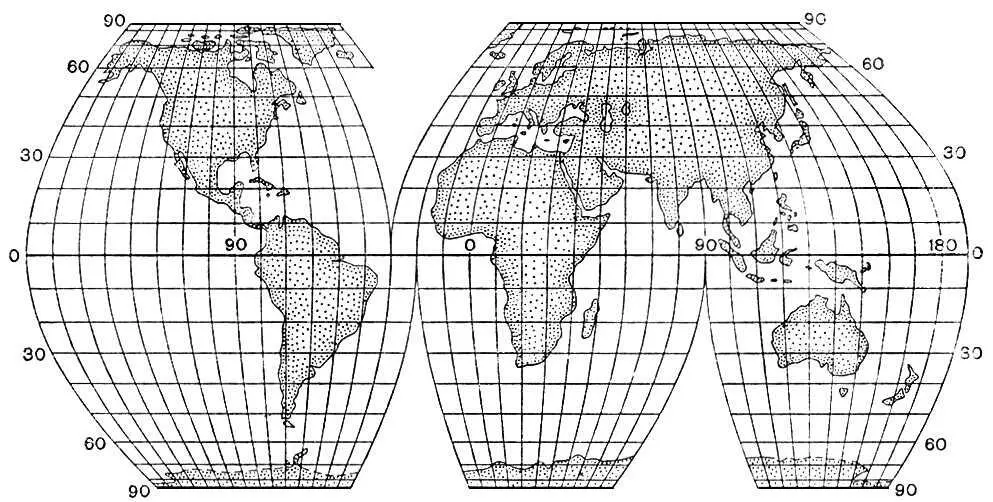
Рис. 8г. Псевдоцилиндрические проекции. Проекция БСАМ.

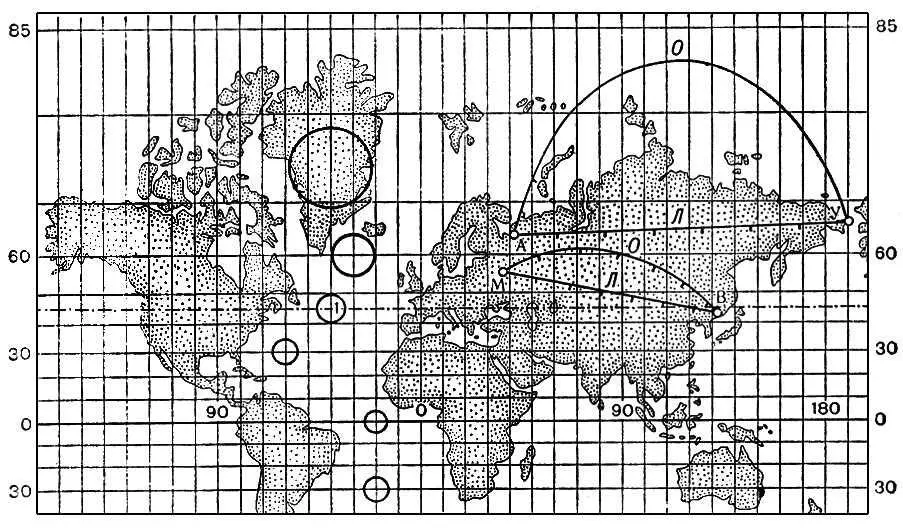
3а. Цилиндрические проекции. Равноугольная Меркатора.

1. Сети сферических координатных линий.