БСЭ БСЭ - Большая Советская Энциклопедия (МО)

Основной М. размером в 10 см, производные от него укрупнённые (3 М., 6 М., 12 М., 15 М., 30 М., 60 М.) и дробные М. вместе с правилами их применения составляют модульную систему. Они установлены советскими, зарубежными и международными нормами и стандартами.

Лит.: Хазанов Д. Б., Модуль в архитектуре, в сборнике: Вопросы теории архитектурной композиции, [в.] 2, М., 1958; Архитектура жилого комплекса, М., 1969.

Д. Б. Хазанов.

Мо'дульв математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число 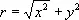(корень берётся со знаком плюс). При представлении комплексного числа z в тригонометрической форме z = r (cos j + i sin j) действительное число r равно М. числа z . М. допускает следующее геометрическое истолкование: комплексное число z = х + iy можно изобразить вектором, исходящим из начала прямоугольной системы координат и имеющим конец в точке с координатами ( х, у ); длина этого вектора и есть М. комплексного числа z .

2) М. перехода от системы логарифмов при основании а к системе логарифмов при основании b есть число М = 1/log a b ; для получения логарифмов чисел х при основании b , если известны логарифмы этих чисел при основании а , надо последние умножить на М. перехода:

log b x = М log a x .

Мо'дульв электронике, унифицированный функциональный узел, функционально законченный узел радиоэлектронной аппаратуры, оформленный конструктивно как самостоятельное изделие. По конструкции М. разделяют на плоские, объёмные и объёмно-плоскостные, по типу электронных приборов — на транзисторные и ламповые. Чаще всего М. собирают на печатных платах . Технология изготовления М. допускает высокую степень автоматизации, что обеспечивает высокую надёжность М. в работе. М. могут быть отдельно настроены и проверены, что позволяет при ремонте производить их замену без дополнительных подстроек и регулировок. Применение М. (функционально-узловой метод конструирования) сокращает сроки проектирования, удешевляет проектирование и изготовление аппаратуры, упрощает её эксплуатацию и модернизацию.

Лит.: Гусев В. П., Технология радиоаппаратостроения, М., 1972.

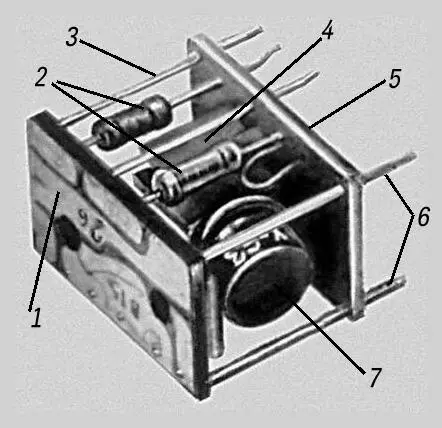
Рис. 2. Объёмный модуль (без кожуха) — усилитель звуковой частоты: 1 — верхняя печатная плата; 2 — резисторы; 3 — металлическая перемычка между печатными платами; 4 — конденсатор; 5 — нижняя печатная плата; 6 — выводы; 7 — транзистор.

Рис. 1. Плоский модуль — логическая ячейка узла электронной вычислительной машины: 1 — выводы; 2 — полупроводниковый диод; 3 — транзистор; 4 — конденсатор; 5 — печатная плата (основание модуля); 6 — резистор.

Мо'дуль высокоэласти'ческий,мера сопротивления деформированию резин и др. каучукоподобных материалов, представляющая собой отношение напряжения s к обратимой деформации e. При малых e величина s пропорциональна e (линейная область механического поведения материала), и поэтому здесь, по определению, М. в. аналогичен обычному модулю продольной упругости (модулю Юнга) или модулю сдвига (см. Модули упругости ) в зависимости от того, при каком виде напряжённого состояния измеряется М. в. При больших e (обычно называемых высокоэластическими) пропорциональность s и e нарушается, и под М. в. в этом случае понимают эквивалентную величину, зависящую от e и по-прежнему определяемую как отношение s/e. М. в. обычно составляет от долей Мн/м 2 до нескольких Мн/м 2(от долей кгс/см 2до десятков кгс/см 2) , тогда как, например, для металлов и полимерных стекол модуль Юнга достигает величин порядка 10 5или 10 3 Мн/м 2соответственно (10 6или 10 4 кгс/см 2). Теоретически М. в. должен возрастать с повышением температуры линейно, практически температурной зависимостью М. в. можно пренебречь. Для высокоэластического состояния характерно отсутствие изменений объёма при растяжении, поэтому М. в., измеренный при сдвиге, составляет 1/ 3М. в., определённого при одноосном растяжении.

Резкая разница значений М. в. каучукоподобных веществ и модуля Юнга кристаллических тел и стекол связаны с различием природы деформаций. Определяющим фактором в случае высокоэластической деформации является гибкость полимерной цепи: деформация тела в целом осуществляется прежде всего путём изменения конформаций макромолекул (см. Высокоэластическое состояние ) . Упругая же деформация происходит вследствие изменения межатомных расстояний и валентных углов. Силы упругости, препятствующие таким изменениям, существенно больше, чем силы, необходимые для предотвращения упругого восстановления каучукоподобного тела. Абсолютные значения М. в. возрастают по мере усиления межмолекулярного взаимодействия полимерных цепей и увеличения густоты пространственной сетки химических связей.

А. Я. Малкин.

Мо'дуль зу'бчатого колеса',геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности d дк числу зубьев z или отношению шага t по делительной окружности к числу: m = d д /z = ts /p. Для косозубых цилиндрических колёс различают: окружной модуль m s = d д /z = ts /p, нормальный модуль m n = t n /p, осевой модуль m a = t а /p, где t s, t n и t a — соответственно окружной, нормальный и осевой шаги по делительному цилиндру. Значения М. з. к. стандартизованы, что является основой для стандартизации других параметров зубчатых колёс (геометрические размеры зубчатых колёс выбираются пропорционально модулю) и зуборезного инструмента (см. Зубчатая передача ) .

Мо'дуль расстоя'ния,разность между видимой ( m ) и абсолютной ( М ) звёздными величинами небесного светила, применяемая в астрономии для описания расстояний до звёзд и звёздных систем. В то время как М зависит только от собственной светимости звезды, m зависит также и от расстояния r (в пс ) до неё: m — М = 5 lg r — 5.

Мо'дуль Ю'нга,то же что, модуль продольной упругости Е ; см. Модули упругости.