БСЭ БСЭ - Большая Советская Энциклопедия (МО)

w = w 0+ Dw cos W t , (3)

где cos W t — модулирующий сигнал, Dw — т. н. девиация частоты. При частотной модуляции полоса частот модулированного колебания зависит от величины b = Dw/W, называемой индексом частотной модуляции. При b << 1 справедливо приближённое соотношение:

х » А 0(sin w t + b sin W t cos w t). (4)

В этом случае частотно-модулированное колебание, так же как и амплитудно-модулированное, состоит из несущей частоты w и двух спутников с частотами w + W и w — W. Поэтому при малых b полосы частот, занимаемые амплитудно-модулированным и частотно-модулированным сигналами, одинаковы. При больших индексах b спектр боковых частот значительно увеличивается. Кроме колебаний с частотами w ± W, появляются колебания, частоты которых равны w ± 2 W, w ± 3 W и т. д. Полная ширина полосы частот, занимаемая частотно-модулированным колебанием с девиацией Dw и частотой модуляции W (с точностью, достаточной для практических целей), может считаться равной 2 Dw + 2 W. Эта полоса всегда шире, чем при амплитудной модуляции.

Преимуществом частотной модуляции перед амплитудной в технике связи является большая помехоустойчивость. Это качество частотной модуляции проявляется при b >> 1, т. е. когда полоса частот, занимаемая частотно-модулированным сигналом, во много раз больше 2 W. Поэтому частотно-модулированные колебания применяются для высококачественной передачи сигналов в диапазоне ультракоротких волн (УKB), где на каждую радиостанцию выделена полоса частот, в 15—20 раз большая, чем в диапазоне длинных, средних и коротких волн, на которых работают радиостанции с амплитудной модуляцией. Частотная модуляция применяется также для передачи звукового сопровождения телевизионных программ. Частотно-модулированные колебания могут быть получены изменением частоты задающего генератора (см. Радиопередатчик ) .

В случае фазовой модуляции модулированное колебание имеет вид:

х = А 0sin (w 0t + Dj cos W t). (5)

Если модулирующий сигнал синусоидальный, то форма модулированных колебаний и их спектральный состав для частотной и фазовой модуляции одинаковы. В случае несинусоидального модулирующего сигнала это различие четко выражено.

В многоканальных системах связи в качестве переносчика информации используется не гармоническое колебание, а периодическая последовательность радиоимпульсов, каждый из которых представляет собой цуг колебаний высокой частоты ( рис. 3 ). Периодическая последовательность таких импульсов определяется четырьмя основными параметрами: амплитудой, частотой следования, длительностью (шириной) и фазой. В соответствии с этим возможны четыре типа импульсной модуляции: амплитудно-импульсная, частотно-импульсная, широтно-импульсная, фазово-импульсная ( рис. 4 ). Импульсная модуляция обладает повышенной помехоустойчивостью по сравнению с модуляцией непрерывной синусоидальной несущей, зато полоса частот, занимаемая передающей радиостанцией с импульсной модуляцией, во много раз шире, чем при амплитудной модуляции (см. Импульсная модуляция, Импульсная радиосвязь ) .

Лит.: Харкевич А. А., Основы радиотехники, ч. 1, М., 1962; Гольдман С., Гармонический анализ, модуляция и шумы, пер. с англ., М., 1951; Рытов С. М., Модулированные колебания и волны, «Тр. Физического института АН СССР», 1940, т. 2, в. 1.

В. Н. Парыгин.

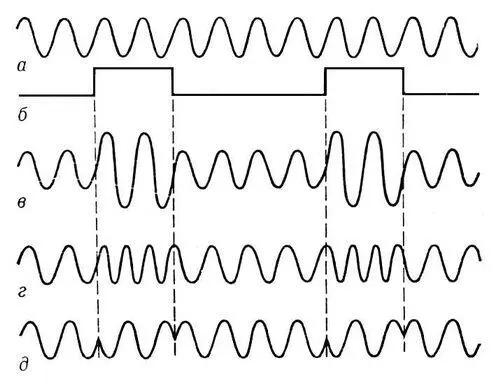
Рис. 1. Схематическое изображение модулированных колебаний: а — немодулированное колебание; б — модулирующий сигнал; в — амплитудно-модулированное колебание; г — частотно-модулированное колебание; д — фазово-модулированное колебание.

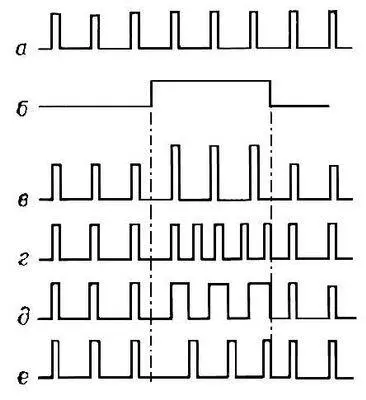
Рис. 4. Различные виды импульсной модуляции: а — немодулированная последовательность радиоимпульсов; б — передаваемый сигнал; в — амплитудно-импульсная модуляция; г — частотно-импульсная модуляция; д — широтно-импульсная модуляция; е — фазово-импульсная модуляция.

Рис. 3. Радиоимпульс.

Рис. 2. Амплитудная модуляция синусоидальным сигналом, w — несущая частота, W — частота модулирующих колебаний, А макси А мин— максимальное и минимальное значения амплитуды.

Модуля'ция све'та, модуляция колебаний электромагнитного излучения оптического диапазона (видимого света, ультрафиолетового и инфракрасного излучений). При М. с. изменяются амплитуда (и следовательно, интенсивность), фаза, частота или поляризация световых колебаний. В любом из этих случаев в конечном счёте меняется совокупность частот, характеризующая излучение, — его гармонический состав. М. с. позволяет «нагружать» световой поток информацией, которая переносится светом и может быть затем извлечена и использована. В принципе количество информации, которое можно передать, модулируя колебания какого-либо вида, тем более велико, чем выше частота этих колебаний (в частности, потому, что с возрастанием частоты модулируемых колебаний — т. н. несущей частоты — появляется возможность увеличить ширину полосы частот модулирующих сигналов; частоты модулирующих колебаний должны быть меньше несущей). Частоты видимого света 10 15—10 16 гц, а всего диапазона оптического излучения — от 10 12до 10 20 гц, т. е. значительно выше, чем у других колебаний, модулируемых с целью передачи информации. Это (а также нередко невозможность решить техническую или научную задачу, не используя оптическое излучение) обусловливает важность и перспективность М. с.

Во многих технических применениях частота модулирующего сигнала настолько мала по сравнению с частотой используемого оптического излучения, что изменение его гармонического состава пренебрежимо мало, и под М. с. понимают периодическое или непериодическое изменение лишь интенсивности излучения. Простейшим, известным с древности примером такой М. с. является световая сигнализация с прерыванием светового потока. В современной технике при подобной М. с. часто важна форма оптических сигналов, которую выбирают наиболее удобной для выполнения конкретной задачи. Это могут быть кратковремеменные импульсы света, сигналы, близкие к прямоугольным, гармоническим и т. д.

Т. н. естественная М. с. происходит уже при испускании света элементарными излучателями (атомами, молекулами, ионами). Конечность времени «высвечивания» таких излучателей (~ 10 -8—10 -9 сек ) приводит к некоторому разбросу частот испускаемого ими излучения (см. Монохроматический свет ) . Естественная М. с. имеет место также при рассеянии света и различных взаимодействиях излучателей между собой. Она позволяет изучать процессы как в отдельных излучателях, так и в их системах (см., например, Комбинационное рассеяние света, Мандельштама — Бриллюэна рассеяние ) .