БСЭ БСЭ - Большая Советская Энциклопедия (ПО)

Соч.: Клинические лекции (о болезнях сердца и их лечении), пер. с франц., СПБ 1898.

Лит.: Менье Л., История медицины, пер. с франц., М. — Л., 1926, с. 193; Vaquez М. Н., Pierre-Carl Potain (1825—1901), «Bulletin de l'Akadémie de médicine», 1927, 3 sér., t. 98, № 41.

Потенциа'л де'йствия(физиологический), быстрое колебание мембранного потенциала, возникающее при возбуждении нервных и мышечных клеток (волокон); активный электрический сигнал, с помощью которого осуществляется передача информации в организме человека и животных. Основан на быстро обратимых изменениях ионной проницаемости клеточной мембраны (см. Биоэлектрические потенциалы ) , связанных с активацией и инактивацией ионных мембранных каналов. В нервных волокнах восходящая фаза П. д. связана с активацией т. н. быстрых натриевых каналов (БНК), а нисходящая фаза — с инактивацией БНК и активацией калиевых каналов (КК). На таком же механизме основана генерация П. д. в волокнах скелетных мышц позвоночных. В мышечных волокнах сердца активация БНК обеспечивает только начальный подъём П. д. Характерное же для этих волокон плато П. д. связано с активированием медленных натрий-кальциевых каналов (МНК). В мембранах волокон гладких мышц внутренних органов и сосудов позвоночных, а также мышечных волокон членистоногих (ракообразных, насекомых) и ряда нейронов моллюсков БНК не обнаружены. П. д. в этих клетках связан с активацией МНК или медленных кальциевых каналов (МКК). Нисходящая фаза П. д. обеспечивается КК.

Изучение физико-химических свойств ионных каналов важно не только для расшифровки их молекулярной структуры, но и для разработки методов управления генерацией П. д. в различных клетках. Установлено, что БНК специфически блокируются тетродотоксином (ядом японской рыбы-шар и калифорнийских саламандр), а также новокаином, кокаином и др. местными анестезирующими средствами. МНК и МКК к этим агентам нечувствительны, но блокируются ионами Mn 2+, Со 2+, Ni 2+, La 3+и органическими соединениями — изоптином (используемым в кардиологической практике) и его дериватом Д-600. Большинство КК эффективно блокируется тетраэтиламмонием. Пусковое влияние П. д. на такие внутриклеточные процессы, как сокращение миофибрилл (в скелетных, гладких и сердечной мышцах), нейросекреция (в некоторых специализированных нейронах и нервных окончаниях) и т.д., осуществляется в результате прямого воздействия электрического импульса; на внутриклеточные структуры (выброс) ионов Ca 2+из саркоплазматической сети мышцы) и влияния на эти структуры ионов Ca 2+ , проникающих внутрь клетки во время П. д.

Лит. см. при ст. Биоэлектрические потенциалы.

Б. И. Ходоров.

Потенциа'л зажига'ния,см. Зажигания потенциал.

Потенциа'л запа'здывающий,см. Запаздывающие потенциалы.

Потенциа'л иониза'ции,см. Ионизационный потенциал.

Потенциа'л,потенциальная функция, понятие, характеризующее широкий класс физических силовых полей (электрическое, гравитационное и т.п.) и вообще поля физических величин, представляемых векторами (поле скоростей в жидкости и т.п.). В электростатическое поле П. вводится как вспомогательная функция, пространственные производные которой — компоненты напряжённости электрического поля в данной точке; в гидродинамике — компоненты скорости в данной точке и т.п. При этом П. в ряде случаев имеет и др. важный физический смысл. Так, в электростатическом поле он численно равен энергии, необходимой для удаления единичного положительного заряда из данной точки в бесконечность (с обратным знаком).

В общем случае П. векторного поля а ( х, у, z ) — скалярная функция u ( х, у, z ) , такая, что а = grad u, т. е. 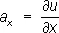, , 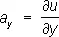, 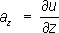где a x, a y, a z; — компоненты поля a в системе декартовых координат Oxyz. Если такую функцию можно ввести, то векторное поле а называют потенциальным. Иногда П. называют функцию U = — u (например, в электростатике). П. векторного поля а определяется не однозначно, а с точностью до постоянного слагаемого. Поэтому при изучении потенциального поля представляют интерес лишь разности П. в различных точках поля. Уравнение u ( х, у, z ) = с геометрически представляет поверхность, во всех точках которой П. имеет одинаковую величину; такие поверхности называют поверхностями уровня, или эквипотенциальными поверхностями.

Для поля тяготения, образованного помещенной в точку A (x, h, x) точечной массой m, П. (ньютонов П.) имеет в точке Р ( х, у, z ) вид:

u ( х, у, z ) = Gm/r, (1)

где 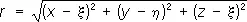, G — постоянная тяготения. При наложении полей их П. алгебраически складываются. Если поле тяготения обусловлено некоторой массой плотности r(x, h, x), занимающей объём Т, то его можно рассматривать как результат наложения элементарных полей, образованных бесконечно малыми телами массы r d x d h d x . Ньютонов П. такого поля представляется интегралом

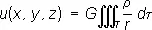. (2)

П. u ( х, у, z ) — непрерывная функция во всём пространстве вместе со своими частными производными 1-го порядка; вне тела объёма Т функция u ( х, у, z ) удовлетворяет Лапласа уравнению, внутри — Пуассона уравнению.

Если притягивающие массы распределены с плотностью r повпо поверхности S (простой слой), то П. образованного ими поля выражается интегралом

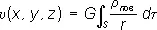. (3)

П. простого слоя u( x, у, z ) — непрерывная во всём пространстве функция; при пересечении поверхности S нормальная производная функции w( х, у, z ) испытывает разрыв, равный 4pG/r пов. Неограниченно сближая две поверхности, на которых расположены простые слои с плотностями r пови —r пов, и одновременно увеличивая r повдо бесконечности, но так, чтобы был конечным предел 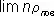= m, где n — нормальное расстояние между поверхностями, приходят к понятию П. двойного слоя:

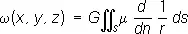(4)