БСЭ БСЭ - Большая Советская Энциклопедия (ПО)

В = rot А ,

E = -gradj 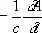, (1)

где с — скорость света в вакууме.

Уравнения для потенциалов поля имеют более простую форму, чем исходные Максвелла уравнения, и поэтому введение П. э. п. упрощает задачу нахождения переменных электромагнитных полей. Существенное упрощение уравнений для П. э. п. возможно благодаря тому, что потенциалы определяются неоднозначно. Если вместо А и j выбрать новые потенциалы

А' = А + gradc ,

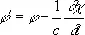, (2)

где c — произвольная функция координат и времени, то векторы В и Е, определяемые уравнениями (1), не изменятся. Инвариантность электромагнитного поля по отношению к преобразованиям потенциалов (2) носит название калибровочной или градиентной инвариантности. Калибровочная инвариантность позволяет наложить на П. э. п. дополнительное условие. Обычно таким дополнительным условием является условие Лоренца:

div A + 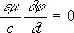, (3)

где e и m— диэлектрическая и магнитная проницаемости среды. При использовании условия (3) уравнения для П. э. п. в однородной среде (e = const, m = const), получаемые из уравнений Максвелла, приобретают одинаковую форму:

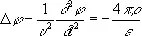, (4)

;

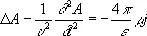здесь D— Лапласа оператор, r и j — плотности заряда и тока, a u = 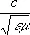— скорость распространения электромагнитного поля в среде. Если r = 0 и j = 0 , то П. э. п. удовлетворяют волновым уравнениям.

Уравнения (4) позволяют определить потенциалы А и j по известному распределению зарядов и токов, а следовательно, с помощью формул (1) — характеристики электромагнитного поля В и Е. Частные решения уравнений (4), удовлетворяющие причинности принципу, называют запаздывающими потенциалами. Запаздывающие потенциалы в точке с координатами х, у, z в момент времени t определяются плотностями заряда и тока в точке с координатами х’, у’, z' в предшествующий момент времени t = t — R/ u , где

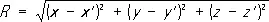
— расстояние от источника поля до точки наблюдения.

Если заряды и токи распределены в конечной области пространства G, то запаздывающие потенциалы определяются суммированием (интегрированием) элементарных потенциалов от зарядов и токов, сосредоточенных в бесконечно малых объёмах dx'dy'dz’, с учётом времени запаздывания:

j ( х, у, z, t ) = ,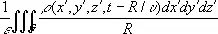

A ( х, у, z, t ) = ,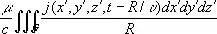

Через П. э. п. выражается функция Гамильтона Н заряженной частицы, движущейся в электромагнитном поле:

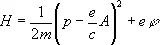, (6)

где p — импульс частицы, e и m — ее заряд и масса. Соответственно через П. э. п. выражается оператор Гамильтона (гамильтониан) в квантовой механике.

Лит. см. при ст. Максвелла уравнения.

Г. Я. Мякишев.

Потенциа'льная эне'ргия,часть общей механической энергии системы, зависящая от взаимного расположения частиц, составляющих эту систему, и от их положений во внешнем силовом поле (например, гравитационном; см. Поля физические ) . Численно П. э. системы в данном её положении равна работе, которую произведут действующие на систему силы при перемещении системы из этого положения в то, где П. э. условно принимается равной нулю (П = 0). Из определения следует, что понятие П. э. имеет место только для консервативных систем, т. е. систем, у которых работа действующих сил зависит только от начального и конечного положения системы. Так, для груза весом Р, поднятого на высоту h, П. э. будет равна П = Ph (П = 0 при h = 0); для груза, прикрепленного к пружине, П = 0,5 с l 2, где l — удлинение (сжатие) пружины, с — её коэффициент жёсткости (П = 0 при l = 0); для двух частиц с массами m 1 и m 2, притягивающихся по закону всемирного тяготения, П = —fm 1m 2/r, где f — гравитационная постоянная, r — расстояние между частицами (П = 0 при r = ¥); аналогично определяется П. э. двух точечных зарядов e 1 и e 2.

С. М. Тарг.

Потенциа'льная я'мав физике, ограниченная область пространства, в которой потенциальная энергия частицы меньше, чем вне её. Термин «П. я.» происходит от вида графика, изображающего зависимость потенциальной энергии V частицы, находящейся в силовом поле, от её положения в пространстве (в случае одномерного движения — от координаты х; рис. 1 ). Такая форма зависимости V ( x ) возникает в поле сил притяжения. Характеристики П. я. — ширина (расстояние, на котором проявляется действие сил притяжения) и глубина (равная разности потенциальных энергий частицы на «краю» ямы и на её «дне», соответствующем минимальной потенциальной энергии). Основное свойство П. я. — способность удерживать частицу, полная энергия E которой меньше глубины ямы V 0 ; такая частица внутри П. я. будет находиться в связанном состоянии.

В классической механике частица с энергией E < V 0 не сможет вылететь из П. я. и будет всё время двигаться в ограниченной области пространства внутри ямы; устойчивому равновесию отвечает положение частицы на «дне» ямы (оно достигается при кинетической энергии частицы Екин = E — V = 0). Если же E > V 0, то частица преодолеет действие сил притяжения и покинет яму. Примером может служить движение упругого шарика, находящегося в поле сил земного притяжения, в чашке с пологими стенками ( рис. 2 ).

В квантовой механике, в отличие от классической, энергия частицы, находящейся в связанном состоянии в П. я., может принимать лишь определённые дискретные значения, т. е. существуют дискретные уровни энергии (см., например, рис. 6 к ст. Квантовая механика ) . Однако такая дискретность уровней становится заметной лишь для систем, имеющих микроскопические размеры и массы. По порядку величины расстояние D E между уровнями энергии для частицы массы m в «глубокой» яме ширины а определяется величиной D E ~ 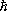/ma 2 ( 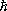— Планка постоянная ) . Наинизший (основной) уровень энергии лежит выше «дна» П. я. (см. Нулевая энергия ) . В П. я. малой глубины ( V o £ 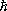/ma 2 ) связанное состояние может вообще отсутствовать (так, протон и нейтрон с параллельными спинами не образуют связанной системы, несмотря на существование сил притяжения между ними).