БСЭ БСЭ - Большая Советская Энциклопедия (РИ)

Геодезическая кривизна(первая кривизна) кривой L в точке М оценивает её отклонение от геодезической L 0, касающейся L в точке М, и определяется следующим образом. Пусть касательный вектор к L в точке М параллельно перенесён в точку M' и образует там угол j с касательной к L в точке М, пусть s — длина дуги MM' кривой L. При стремлении M' к М существует предел

,

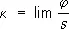который и называется геодезической кривизной кривой L в точке М. Аналитически геодезическая кривизна кривой x I = x i ( s ), параметризованной длиной дуги, определяется формулами:

,

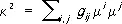где

;

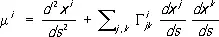таким образом, геодезическая кривизна кривой L совпадает с (первой) кривизной её развёртки L, а геодезические линии во всех точках имеют нулевую геодезическую кривизну.

Для кривой L в римановом пространстве R определяются также вторая и т.д. кривизны и имеют место соотношения, аналогичные обычным формулам Френе (см. Дифференциальная геометрия) для кривых евклидова пространства.

Риманова кривизна.Пусть М — точка риманова пространства, F — двумерная поверхность x i = x i ( u, u) , проходящая через М, L — простой замкнутый контур на F, проходящий через М, s — площадь участка поверхности, ограниченного контуром L. Пусть произвольный вектор a i, касательный к поверхности F (т. е. линейно выражающийся через векторы 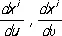) , перенесен параллельно по L.

Тогда составляющая перенесённого вектора, касательная к F, окажется повёрнутой по отношению к a i на угол j (положительное направление отсчёта углов должно совпадать с направлением обхода L ). При стягивании L в точку М существует предел

,

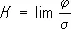называется кривизной риманова пространства (римановой кривизной) в данной точке в направлении двумерной поверхности; К зависит не от поверхности, а лишь от её направления в точке М, т. е. от направления двумерной плоскости касательного евклидова пространства, содержащей векторы .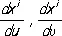

Риманова кривизна К связана с тензором кривизны формулой:

,

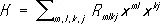где

,

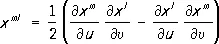причём параметры u, u выбраны так, что площадь параллелограмма, построенного на векторах 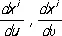, равна 1.

В двумерном случае К совпадает с полной кривизной (Theorema egregium К. Ф. Гаусса, 1827), при этом для области G , ограниченной простой замкнутой кривой Г, имеющей геодезическую кривизну k, справедлива так называемая формула Гаусса-Бонне:

,

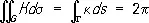в частности, для треугольника, образованного отрезками геодезических

,

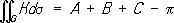где А, В, С — величины углов треугольника. Для замкнутого (т. е. без границы) двумерного риманова пространства R его эйлерова характеристика c( R ) пропорциональна интегралу римановой кривизны:

.

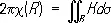Эта формула обобщена на случай чётно-мерного замкнутого риманова пространства, в котором интегрируется некоторая функция компонент тензора кривизны.

Если в каждой точке риманова пространства кривизна не зависит от направления двумерной поверхности, то она не меняется и от точки к точке, т. е. пространство имеет постоянную кривизну. Представляют интерес также (в частности, для описания механических систем с циклическими координатами) римановы пространства со специальной структурой тензора кривизны; они суть обобщение пространств постоянной кривизны и имеют достаточно обширную группу движений. Таковы, например, симметрические пространства, характеризующиеся тем, что их тензор кривизны не меняется при параллельном перенесении, субпроективные пространства, характеризующиеся специальной координатной системой, в которой геодезические описываются линейными уравнениями, и др.

Риманова кривизна играет важную роль в геометрических приложениях Р. г., тем более, что на всяком многообразии можно ввести некоторую риманову метрику. Так, например, топологическое строение полных римановых пространств (т. е. пространств, в которых всякая геодезическая бесконечно продолжаема) зависит от свойств его кривизны: всякое полное односвязное n -мерное риманово пространство гомеоморфно n -мерному евклидову пространству, если его кривизна во всех точках и по всем направлениям неположительна и гомеоморфна n -мерной сфере единичного радиуса, если его кривизна К удовлетворяет неравенствам 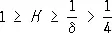, где d — некоторая постоянная. От величины кривизны полного риманова пространства R зависит и его диаметр d — точная верхняя грань расстояний между точками R, определяемых внутренней метрикой R: например, если К ³ K o > 0 , то 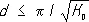d, если же , то R — сфера радиуса .

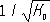Метрическая связность.Параллельное перенесение вдоль кривой L с концами А, В задаёт изометричное (т. е. сохраняющее расстояния) преобразование t iкасательного пространства E Aв точке А в касательное пространство E Bв точке А. Дифференциал преобразования t iв точке А, т . е. главная линейная часть изменения t i; при переходе из А ( xi ) в близкую точку 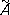( x i + dx i ) , определяет некоторый геометрический объект, называется римановой связностью, ассоциированной с данным параллельным перенесением. Аналитически эта связность выражается системой линейных дифференциальных форм