БСЭ БСЭ - Большая Советская Энциклопедия (РИ)

Простейшие понятия римановой геометрии.1) Длина дуги s кривой ( i = 1, …, n , 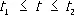) в римановом пространстве R определяется как интеграл

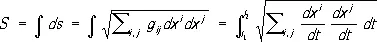
вдоль этой кривой (что соответствует как бы измерению длин «малым масштабом», как отметил ещё Риман). Если любые две точки пространства R соединимы кривой, то R становится метрическим пространством: расстояние r( Х, Y ) между двумя точками определяется как точная нижняя грань длин кривых, соединяющих эти точки, и называется внутренней метрикой риманова пространства R.

2) Угол между двумя исходящими из одной точки А кривыми определяется как угол между касательными векторами к кривым в точке А.

3) Объём V n -мерной области G риманова пространства определяется по формуле:

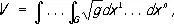где .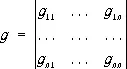

Геодезические.Линии, которые в достаточно малых областях являются кратчайшими из всех кривых с теми же концами, называются геодезическими, они играют роль прямых в римановом пространстве R. По определению, они являются экстремалями функционала

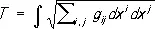
(см. Вариационное исчисление ) и удовлетворяют уравнениям:

,

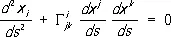где Г i jk — так называемые Кристоффеля символы, выражающиеся через компоненты метрического тензора g ij и их первые производные. Через каждую точку риманова пространства в любом направлении проходит геодезическая; любые две точки А, В достаточно малой области можно соединить кратчайшей [длина её будет равна внутреннему расстоянию r( А, В ) между этими точками], и притом единственной, однако единственность может нарушаться, если точки достаточно удалены друг от друга (например, полюсы сферы соединимы бесконечным множеством дуг больших кругов, являющихся кратчайшими).

Представляет интерес (для описания периодических движений в механической задаче многих тел, например) оценка числа n замкнутых геодезических пространства R ; эта задача (поставленная Ж. А. Пуанкаре в 1905 в связи с некоторыми вопросами небесной механики), несмотря на усилия многих математиков, ещё далека от завершения, наилучший результат: n ³ 2, если R односвязно.

Соприкасающееся пространство.Между римановым пространством R и касательным к нему евклидовым пространством в окрестности U некоторой точки А можно установить такое соответствие, при котором оба пространства будут совпадать с точностью до малых выше второго порядка. Для этого проводят из точки А геодезические во всех направлениях и каждой из них в касательном пространстве сопоставляют луч соответствующего направления, а затем устанавливают такое соответствие этих лучей и геодезических, при котором длины дуг геодезических b соответствующих им лучей равны. В достаточно малой окрестности такое соответствие будет взаимно однозначным; если ввести в касательном пространстве декартовы координаты x 1,..., x n и приписать их значения соответствующим точкам окрестности U, то между линейными элементами ds риманова и ds o евклидова пространств будет такая связь:

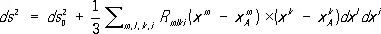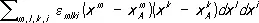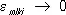+ , где при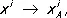

i = 1, …, n .

откуда следует, что разность ds — ds o имеет порядок не ниже, чем

.

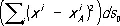Евклидово пространство, поставленное в такое соответствие с римановым, и называется соприкасающимся (в отличие от обычного касательного пространства). Добиться более высокого порядка совпадения за счёт специального выбора соответствия между римановым и евклидовым пространствами в общем случае уже невозможно. Поэтому коэффициенты R mlki характеризуют отличие риманова пространства от евклидова; они являются компонентами так называемого тензора кривизны (или тензора Римана — Кристоффеля), определяемого по формуле

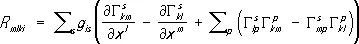
лишь через g ik, и их производные до второго порядка.

Тождественное обращение в нуль тензора кривизны необходимо и достаточно для того, чтобы пространство в окрестности каждой точки совпадало с евклидовым (в целом оно может отличаться от него своим строением, подобно тому как боковая поверхность цилиндра отличается от плоскости).

Параллельное перенесение.Для всякой гладкой кривой L риманова пространства существует отображение её окрестности U L в евклидово пространство E L при котором оно оказывается соприкасающимся во всех точках кривой L. Образ кривой L в пространстве E L называется развёрткой L' этой кривой на евклидово пространство (для поверхности F в евклидовом пространстве соприкасающееся евклидово пространство вдоль кривой L можно интерпретировать как развёрнутую на плоскость огибающую семейства плоскостей, касательных к F вдоль L ) . Вектор (и любой тензор) параллельно переносится вдоль кривой L, если параллельно переносится соответствующий вектор (тензор) в евклидовом пространстве E L, соприкасающемся с римановым вдоль этой кривой. Аналитически параллельное перенесение вектора a i вдоль кривой x i = x i ( t ) определяется дифференциальным уравнением

.

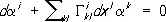Если 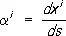, то получается уравнение геодезических; т. о., геодезические можно определить как кривые, вдоль которых касательный к ним вектор переносится параллельно, т. е. развёртка геодезической — прямая, что углубляет их сходство с прямыми. Результат параллельного перенесения вектора из точки А в точку В зависит, как правило, от кривой AB, вдоль которой происходит перенесение, — в этом отсутствии «абсолютного параллелизма» наглядно проявляется отличие риманова пространства от евклидова.