БСЭ БСЭ - Большая Советская Энциклопедия (РИ)

Если в пространстве ввести прямоугольную систему координат x, h, z так, что оси x и h совпадают, соответственно, с осями х и у, то точке x + iy комплексной числовой плоскости соответствует точка

,

,

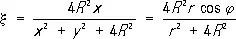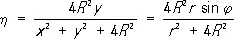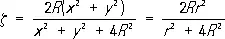
Р. с. (уравнение которой ).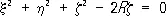

Ри'манова геоме'трия,многомерное обобщение геометрии на поверхности, представляющее собой теорию римановых пространств, т. е. таких пространств, где в малых областях приближённо имеет место евклидова геометрия (с точностью до малых высшего порядка сравнительно с размерами области). Р. г. получила своё название по имени Б. Римана, который заложил её основы в 1854.

Понятие о римановой геометрии.Гладкая поверхность в евклидовом пространстве, рассматриваемая с точки зрения измерений, производимых на ней, оказывается двумерным пространством, геометрия которого (так называемая внутренняя геометрия ) , будучи приближённо евклидовой в малом (в окрестности любой точки она совпадает с точностью до малых высшего порядка с геометрией касательной плоскости), точно не является евклидовой; к тому же, как правило, поверхность неоднородна по своим геометрическим свойствам. Поэтому внутренняя геометрия поверхности и есть не что иное, как Р. г. двух измерений, а сама поверхность есть двумерное риманово пространство.

Так, при измерениях на участках земной поверхности, малых в сравнении с размерами земного шара, можно с успехом применять обычную планиметрию, однако результаты измерений на больших участках обнаруживают существенное отклонение от законов планиметрии. Перенесение этих понятий на многомерные пространства приводит к общей Р. г. В основе Р. г. лежат три идеи. Первая идея — признание того, что вообще возможна геометрия, отличная от евклидовой, — была впервые развита Н. И. Лобачевским, вторая — это идущее от К. Ф. Гаусса понятие внутренней геометрии поверхностей и её аналитический аппарат в виде квадратичной формы, определяющей линейный элемент поверхности; третья идея — понятие об n -мерном пространстве, выдвинутое и разработанное в 1-й половине 19 в. рядом геометров. Риман, соединив и обобщив эти идеи (в лекции «О гипотезах, лежащих в основании геометрии», прочитанной в 1854 и опубликованной в 1867), ввёл общее понятие о пространстве как непрерывной совокупности любого рода однотипных объектов, которые служат точками этого пространства (см. Геометрия, раздел Обобщение предмета геометрии, Пространство в математике), и перенёс на эти пространства представления об измерении длин малыми шагами.

После опубликования работ Римана его идеи привлекли внимание ряда математиков, которые развивали дальше аналитический аппарат Р. г. и устанавливали в ней новые теоремы геометрического содержания. Важным шагом было создание итальянскими геометрами Г. Риччи-Курбастро и Т. Леви-Чивита на рубеже 20 в. так называемого тензорного исчисления, которое оказалось наиболее подходящим аналитическим аппаратом для разработки Р. г. Решающее значение имело применение Р. г. в создании А. Эйнштейном общей теории относительности, которое было триумфом не только абстрактной геометрии, но и идей о связи геометрии и физики, выдвинутых Лобачевским и Риманом. Это привело к бурному развитию Р. г. и её разнообразных обобщений. В настоящее время Р. г. вместе с её обобщениями представляет собой обширную область геометрии, которая продолжает успешно развиваться, причём особое внимание уделяется вопросам глобального характера.

Определение риманова пространства.К строгому определению риманова пространства можно подойти следующим образом. Положение точки n -мерного многообразия определяется n координатами x 1, x 2,..., x n . В евклидовом n -мерном пространстве расстояние между любыми двумя точками X , Y в надлежаще выбранных координатах выражается формулой

где D x i — разности координат точек X, Y. Соответственно в римановом пространстве в окрестности каждой точки А могут быть введены координаты x 1,..., x n так, что расстояние между точками X, Y , близкими к А, выражаются формулой

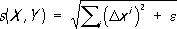
где e таково, что 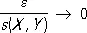, когда X, Y приближаются к А. Отсюда следует, что в произвольных координатах расстояние между близкими точками ( x i ) и ( x i + dx i ) , или, что то же самое, дифференциал длины дуги кривой, задаётся выражением

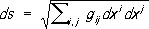
(здесь коэффициенты 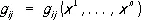суть функции координат), которое называется линейным элементом риманова пространства. Т. о., риманово пространство R можно аналитически определить как n -мерное многообразие, в котором в каждой точке задана дифференциальная квадратичная форма

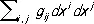
(она называется также метрической формой, или просто метрикой, R и является по своему определению положительно определённой). Возможность преобразования координат обусловливает то, что одно и то же риманово пространство в разных координатах имеет разные выражения метрической формы, однако её величина (вследствие своего геометрического смысла как квадрата элемента длины дуги) при преобразовании координат от x i к 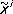должна оставаться неизменной:

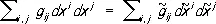
Это приводит к определённому закону преобразования коэффициентов g ij как компонент дважды ковариантного тензора (см. Тензорное исчисление ) ; он называется метрическим тензором риманова пространства.

Каждой точке А риманова пространства R сопоставляется так называемое касательное евклидово пространство E A, в которое отображается некоторая окрестность U точки А так, что относительное искажение расстояний стремится к нулю при приближении к точке А. Аналитически это сводится к введению вблизи некоторой точки A 0 пространства E A таких координат, что в них квадрат линейного элемента 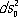евклидова пространства E A выражается в точке A 0 такой же формой 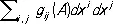, какой выражается квадрат линейного элемента риманова пространства ds 2 в точке А. Т. о., в пренебрежении малыми выше первого порядка окрестность точки в римановом пространстве можно заменять окрестностью точки касательного пространства.