БСЭ БСЭ - Большая Советская Энциклопедия (СП)

Лит.: Курс астрофизики и звездной астрономии, под ред. А. А. Михайлова, 3 изд., т. 1, М., 1973, гл. 18; Cannon A. J. and Picketing Е. C., The Henry Draper catalogue, [v.] 1—9, Camb. (Mass.), 1918—1924 (Annals of the Astronomical observatory of Harvard college, v. 91—99); Morgan W. W., Keenan P.C. and Кellman Е., An atlas of stellar spectra with an outline of spectral classification, Chi., 1943.

Д. Я. Мартынов.

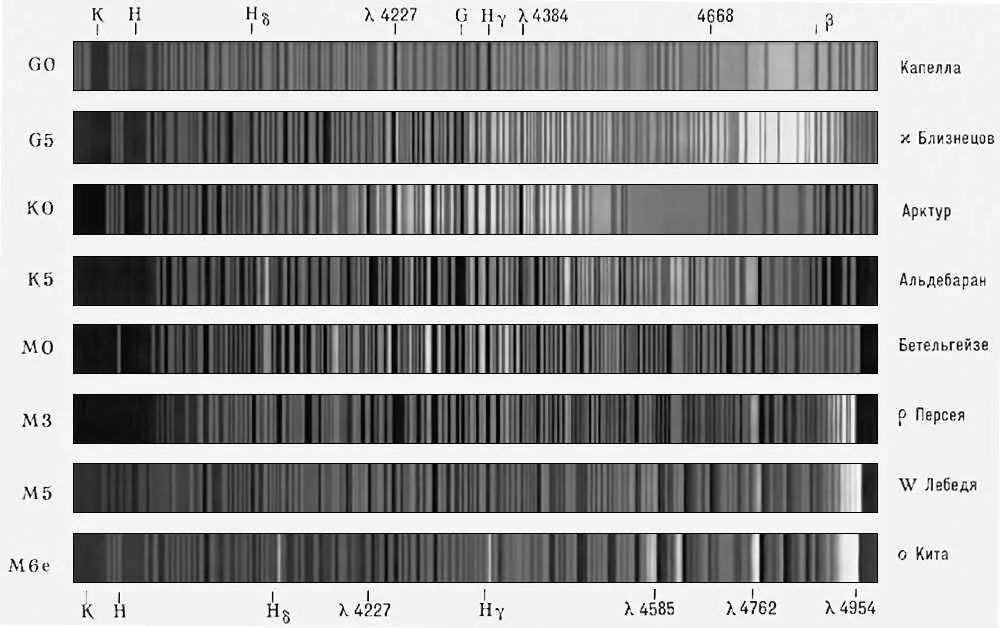
Спектральные классы звёзд G0 — M6e.

Спектральные классы звёзд Oa — F5.

Спектра'льная пло'тностьвеличины, характеризующей излучение (например, потока излучения , силы света ), отношение рассматриваемой величины, взятой в очень (более строго — бесконечно) малом интервале, содержащем данную длину волны l, к ширине этого интервала d l. Вместо l могут использоваться частоты, волновые числа или их логарифмы. В таких случаях термин «С. п.» уточняется — говорят, например, о С. п. по частоте. График зависимости С. п. от длины волны l или частоты n характеризует распределение соответствующей величины по спектру.

Спектра'льная светова'я эффекти'вность(устаревшая видность) излучения в воспринимаемом человеческим глазом («видимом») диапазоне длин волн l (частот n) излучения, отношение светового потока излучения с длиной волны l ( монохроматического света ) к соответствующему потоку излучения . Обозначается К (l). Максимальное значение К т @ 680 лм/вт С. с. э. принимает при l » 555 нм. Величины С. с. э. и относительная С. с. э. (относительная видность) V(l) = К (l)/ К т лежат в основе построения системы световых величин. См. также Световая эффективность , Спектральная чувствительность .

Спектра'льная сенситоме'трия,см. Сенситометрия .

Спектра'льная чувстви'тельность приёмника излучения , отношение величины, характеризующей уровень реакции приёмника, к потоку энергии монохроматического излучения, вызывающего эту реакцию (см. Монохроматический свет ). Различают абсолютную С. ч., выражаемую в именованных единицах (например, a/вm, если реакция приёмника измеряется в амперах ), и безразмерную относительную С. ч. — отношение С. ч. при данной длине волны излучения к максимальному значению С. ч. или к С. ч. при некоторой др. длине волны. С. ч. глаза человека — то же, что и спектральная световая эффективность излучения (видность). О С. ч. фотоматериалов см. в ст. Сенсибилизация оптическая, Сенситометрия .

Спектра'льно-двойные звёзды, двойные звёзды , компоненты которых столь близки между собой, что не видны порознь даже в самые сильные телескопы. Двойственность таких звёзд обнаруживается только по периодическим смещениям либо раздвоениям линий в их спектрах вследствие Доплера эффекта , происходящего вследствие орбитального движения компонентов.

Спектра'льное разложе'ниефункции, разложение функции в ряд по собственным функциям некоторого линейного оператора (например, конечно-разностного, дифференциального или интегрального), действующего в функциональном пространстве, или одно из возможных обобщений такого разложения. Частным случаем С. р. является разложение функции, заданной на конечном отрезке, в Фурье ряд (т. е. гармонический анализ колебаний), а также разложения по другим известным полным системам функций. В случае линейного оператора А, имеющего непрерывный спектр, собственные функции, понимаемые в обычном смысле, не существуют; тем не менее и здесь весьма часто удаётся определить эти функции (но только они уже не будут являться элементами того функционального пространства, в котором действует оператор А) и задать С. р. широкого класса функций как разложение в интеграл по системе функций, зависящей от непрерывно изменяющегося аргумента (пример С. р. этого типа — разложение в Фурье интеграл ) . Для несамосопряжённых операторов А наряду с собственными функциями приходится рассматривать ещё и цепочки функций, присоединённых к собственным функциям; однако и для таких операторов в функциональных пространствах во многих случаях удаётся доказать теорему о полноте системы всех собственных и присоединённых функций и, исходя отсюда, получить С. р. широкого класса функций по всевозможным собственным и присоединённым функциям оператора А.

С. р. функций широко используются для решения различных конечно-разностных, дифференциальных и интегральных уравнений и находят многочисленные приложения в задачах классической механики (особенно теории колебаний), электродинамики, квантовой механики, теории связи, теории автоматического управления и других разделах математической физики и прикладной математики.

Лит.: Березанский Ю. М., Разложение по собственным функциям самосопряженных операторов, К., 1965; Титчмарш Э. Ч., Разложения по собственным функциям, связанные с дифференциальными уравнениями второго порядка, пер. с англ., т. 1—2, М., 1960—61; Наймарк М. А., Линейные дифференциальные операторы, 2 изд., М., 1969; Левитан Б. М., Capгсян И. С., Введение в спектральную теорию (самосопряженные обыкновенные дифференциальные операторы), М., 1970.

А. М. Яглом.

Спектра'льное разложе'ниелинейного оператора, представление линейного оператора А в виде линейной комбинации операторов проектирования на взаимно перпендикулярные оси или (более общо) в виде специального интеграла, содержащего под знаком интегрирования семейство операторов проектирования, удовлетворяющее определённым условиям (так называемое разложение единицы, отвечающее оператору А ). Изучение С. р. и их возможных обобщений для различных типов линейных операторов составляет основное содержание спектрального анализа линейных операторов.

Спектра'льное разложе'ниеслучайной функции, разложение случайной функции (в частности, случайного процесса ) в ряд или интеграл по той или иной специальной системе функций такое, что коэффициенты этого разложения представляют собой взаимно некоррелированные случайные величины. Наиболее известный класс С. р. случайных функций — представления стационарных случайных процессов Х (t) в виде интеграла Фурье — Стилтьеса