БСЭ БСЭ - Большая Советская Энциклопедия (СП)

,

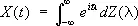где Z(l) — случайная функция с некоррелированными приращениями. Существование такого С. р. показывает, что стационарный случайный процесс всегда можно рассматривать как наложение некоррелированных друг с другом гармонических колебаний различных частот со случайными фазами и амплитудами. С. р. аналогичного вида, но с заменой гармонических колебаний n -мерными плоскими волнами, имеет место и для однородных случайных полей в n -мерном пространстве. Другой тип С. р. случайных функций — это разложение случайного процесса X ( t ) , заданного на конечном отрезке оси (или, более общо, случайной функции X ( t ) , заданной на ограниченной области n -мерного пространства), в ряд вида

,

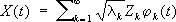где j k ( t ) и l k— собственные функции и собственные значения интегрального оператора в функциональном пространстве с ядром, равным корреляционной функции случайного процесса (или функции) X ( t ) , a Z k, k = 1, 2,..., — последовательность попарно некоррелированных случайных величин единичной дисперсии. С. р. специального вида имеют место также для однородных и изотропных случайных полей в евклидовых пространствах и для однородных полей на пространствах с группой преобразований, отличных от евклидова пространства.

Лит.: Яглом А. М., Спектральные представления для различных классов случайных функций, в кн.; Труды 4-го Всесоюзного математического съезда, т. 1, Л., 1963, с. 250—73: Гихман И. И., Скороход А. В., Теория случайных процессов, т.1, М., 1971.

А. М. Яглом.

Спектра'льные ли'нии,узкие участки в спектрах оптических, каждый из которых можно охарактеризовать определённой длиной волны l (или частотой 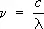, где с — скорость света). С. л.

наблюдаются в спектрах испускания как светлые (цветные) линии на тёмном фоне, в спектрах поглощения — как тёмные линии на светлом фоне (см. рис ). Каждая С. л. соответствует определённому квантовому переходу в атоме (молекуле, кристалле). С. л. не являются строго монохроматичными: каждая С. л. имеет некоторую ширину Dl (см. Ширина спектральных линий ) .

Спектра'льные прибо'ры,приборы для исследования спектрального состава по длинам волн электромагнитных излучений в оптическом диапазоне (10 -3—10 3 мкм; см. Спектры оптические ) , нахождения спектральных характеристик излучателей и объектов, взаимодействовавших с излучением, а также для спектрального анализа. С. п. различаются методами спектрометрии, приёмниками излучения, исследуемым (рабочим) диапазоном длин волн и др. характеристиками.

Принцип действия большинства С. п. можно пояснить с помощью имитатора, изображенного на рис. 1. Форма отверстия в равномерно освещенном экране 1 соответствует функции f (l) , описывающей исследуемый спектр — распределение энергии излучения по длинам волн l. Отверстие в экране 2 соответствует функции а(l—l'), описывающей способность С. п. выделять из светового потока узкие участки dl в окрестности каждой l’ . Эту важнейшую характеристику С. п. называют функцией пропускания, или аппаратной функцией (АФ). Процесс измерения спектра f (l) прибором с АФ а (l — l’) можно имитировать, регистрируя изменения светового потока, проходящего через отверстие, при перемещении (сканировании) экрана 2 относительно экрана 1. Очевидно, чем меньше ширина АФ, тем точнее будет измерена форма контура спектра f (l) , тем более тонкая структура может быть в нём обнаружена.

Ширина АФ наряду с рабочим диапазоном l является основной характеристикой С. п.; она определяет спектральное разрешение dl и спектральную разрешающую способность R = l/dl. Чем шире АФ, тем хуже разрешение (и меньше R ) , но больше поток излучения, пропускаемый прибором, т. е. больше оптический сигнал и М — отношение сигнала к шуму. Шумы (случайные помехи), неизбежные в любых измерительных устройствах, в общем случае пропорциональны 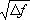(D f — полоса пропускания приёмного устройства). Чем шире D f , тем выше быстродействие прибора и меньше время измерения, но больше шумы (меньше M). Взаимосвязь величин R, М, ( f определяется соотношением:

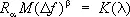. (1)

Показатели степени a и b принимают различные положительные значения в зависимости от конкретного типа С. п. Константа К, зависящая только от l , определяется конструктивными параметрами данного типа С. п. и накладывает ограничения на величины R, М, D f . Кроме того, возможные значения R ограничиваются дифракцией света, аберрациями оптических систем, а значения D f — инерционностью приёмно-регистрирующей части С. п.

Рассмотренный с помощью рис. 1 принцип действия С. п. относится к одноканальным методам спектрометрии. Наряду с ними широко распространены многоканальные методы, в которых сканирование не применяется и излучения различных l регистрируются одновременно. Это соответствует наложению на экран 1 неподвижного экрана с вырезанными N контурами АФ для разных l при независимой регистрации потоков от каждого отверстия (канала).

Общая классификация методов спектрометрии, являющихся основой различных схем и конструкций С. п., представлена на рис. 2 . Классификация дана по двум основным признакам — числу каналов и физическим методам выделения l в пространстве или времени. Исторически первыми и наиболее распространёнными являются методы пространственного разделения l (селективной фильтрации), которые называются «классическими» (группы 1 и 2 на рис. 2 ). В одноканальных С. п. (группа 1) исследуемый поток со спектром f (() посылается на спектрально-селективный фильтр, который выделяет из потока некоторые интервалы dl в окрестности каждой l‘ и может перестраиваться (непрерывно или дискретно), осуществляя сканирование спектра во времени по некоторому закону l’( t ) . Выделенные компоненты dl посылаются на приёмник излучения, запись сигналов которого даёт функцию времени F ( t ) . Переход от аргумента t к аргументу l даёт функцию F (l) — наблюдаемый спектр.

В многоканальных С. п. (группа 2) информация об исследуемом спектре получается путём одновременной регистрации (без сканирования по l) несколлькими приёмниками потоков излучения разных длин волн (l’, l’’, l’’’, ...). Последние выделяют, например, набором узкополосных фильтров или многощелевыми монохроматорами (полихроматорами). Если расстояние между каналами не превышает dl и число каналов N достаточно велико, то получаемая информация аналогична содержащейся в записи спектра на сканирующем одноканальном приборе (при тех же dl , одинаковых приёмниках и пр. равных условиях), но время измерения может быть сокращено в N раз. Наибольшая многоканальность достигается применением многоэлементных фотоэлектрич. приёмников излучения и фотографических материалов (в спектрографах).