БСЭ БСЭ - Большая Советская Энциклопедия (ФУ)

Обычное евклидово пространство является одним из простейших примеров (действительного) гильбертова пространства . Однако в Ф. а. играют основную роль бесконечномерные пространства, т. е. такие, в которых существует бесконечное число линейно независимых векторов. Вот примеры таких пространств, элементами которых являются классы комплекснозначных (т. е. со значениями в 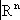, норма || x || = 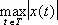; банахово пространство L p ( T ) всех суммируемых с р -й ( p ³ 1) степенью функций на Т , норма 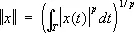; банахово пространство l p всех последовательностей таких, что 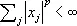, здесь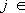 (множеству целых чисел), норма || x || =(å | x j | p ) 1/ p; в случае p = 2 пространства l 2 и L 2 ( T ) гильбертовы, при этом, например, в L 2 ( T ) скалярное произведение 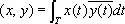; линейное топологическое пространство D ( 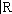), состоящее из бесконечно дифференцируемых функций на 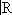, каждая из которых финитна [т. е. равна нулю вне некоторого интервала ( а , b )]; при этом x n 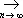x, если x n ( t ) равномерно финитны [т. е. ( а , b ) не зависит от n ] и сходятся равномерно со всеми своими производными к соответствующим производным x ( t ).

Все эти пространства бесконечномерны, проще всего это видно для l 2 : векторы e j = {0,..., 0, 1, 0,...} линейно независимы.

С геометрической точки зрения наиболее простыми являются гильбертовы пространства Н , свойства которых больше всего напоминают свойства конечномерных евклидовых пространств. В частности, два вектора x , у Î Н называются ортогональными ( x ^ y ), если ( x , у ) = 0. Для любого x Î Н существует его проекция на произвольное подпространство F — линейное замкнутое подмножество Н , т. е. такой вектор x F , что x — x F ^ f для любого f Î F . Благодаря этому факту большое количество геометрических конструкций, имеющих место в евклидовом пространстве, переносится на Н , где они часто приобретают аналитический характер. Так, например, обычная процедура ортогонализации приводит к существованию в Н ортонормированного базиса — последовательности векторов e j , j Î 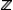, из Н таких, что || e j || = 1, e j ^ e k при j ¹ k , и для любого x Î H справедливо «покоординатное» разложение

x = å x je j (1)

где x j = ( x , e j ), || x || = å | x j | 2(для простоты Н предполагается сепарабельным, т. е. в нём существует счётное всюду плотное множество). Если в качестве Н взять L 2(0, 2p) и положить 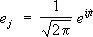, j =...,—1, 0, 1..., то (1) даст разложение функции x ( t ) Î L 2(0, 2p) в ряд Фурье, сходящийся в среднем квадратичном. Кроме того, соотношение (1) показывает, что соответствие между Н и l 2' {xj} , j Î 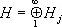гильбертовых пространств H j — конструкция, подобная образованию Н одномерными подпространствами, описываемому формулой (1); факторизация и пополнение: на исходном линейном пространстве Х задаётся квазискалярное произведение [т. е. возможно равенство ( x , x ) = 0 для x ¹ 0], часто весьма экзотического характера, и Н строится процедурой пополнения Х относительно (.,.) после предварительного отождествления с 0 векторов x , для которых ( x , x ) = 0; тензорное произведение 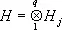— образование его аналогично переходу от функций одной переменной f ( x 1 ) к функциям многих переменных f ( x 1 ,..., x q ); проективный предел 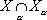банаховых пространств — здесь 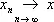(грубо говоря), если 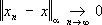для каждого a; индуктивный предел 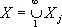банаховых пространств X 1 Ì X 2 Ì..., здесь 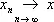, если все x j , начиная с некоторого j 0 , лежат в одном X j0 , и в нём 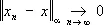. Две последние процедуры обычно применяются для построения линейных топологических пространств. Таковы, например, ядерные пространства — проективный предел гильбертовых пространств Н a, обладающих тем свойством, что для каждого a найдётся b такое, что h bÌ Н a, и это — т. н. вложение Гильберта — Шмидта [D ( 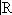) — пример ядерного пространства].

Разработан важный раздел Ф, а., в котором изучаются пространства с конической структурой «x 0» (полуупорядоченностью). Пример такого пространства — действительное С ( Т ), в нём считается x 0, если x ( t ³)0 для всех t Î T .

3. Операторы (общие понятия). Функционалы.Пусть X , Y — линейные пространства; отображение A : X ® Y называется линейным, если для x , у Î X , l, m Î ,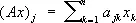

где x 1 ,..., x n и ( Ax ) 1,..., ( Ax ) n — координаты векторов x и Ax соответственно. При переходе к бесконечномерным линейным топологическим пространствам положение значительно усложняется. Здесь прежде всего необходимо различать непрерывные и разрывные линейные операторы (для конечномерных пространств они всегда непрерывны). Так, действующий из пространства L 2 ( а , b ) в него же оператор