Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

Показательная функция вида

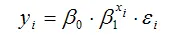
является нелинейной по коэффициенту β1 и относится к классу моделей регрессии, которые можно с помощью преобразований привести к линейному виду. Данная модель характеризуется тем, что случайная ошибка εi мультипликативно связана с факторной переменной хi . Следовательно, для определения оценок неизвестных коэффициентов данной модели можно применить классический метод наименьших квадратов.

Данную модель можно привести к линейному виду с помощью логарифмирования:

Log yi=log β0+ хi* logβ1+ logεi.

Для более наглядного представления данной модели регрессии воспользуемся методом замен:

log yi=Yi;

log β0=A;

logβ1=B ;

logεi=E .

В результате произведённых замен получим окончательный вид показательной функции, приведённой к линейной форме:

Yi=A+Bхi+E .

Таким образом, мы будем применять метод наименьших квадратов не к исходной форме показательной функции, а к её преобразованной форме.

Для определения неизвестных коэффициентов линеаризованной формы показательной функции методом наименьших квадратов необходимо минимизировать сумму квадратов отклонений логарифмов наблюдаемых значений результативной переменной у от теоретических значений ỹ (значений, рассчитанных на основании модели регрессии), т. е. минимизировать функционал МНК вида:

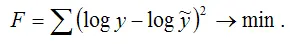
Оценки неизвестных коэффициентов А и В линеаризованной формы показательной функции находятся при решении системы нормальных уравнений вида:

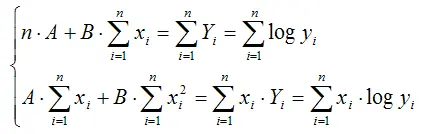
Данная система является системой нормальных уравнений относительно коэффициентов А и В для функции вида Yi=A+Bхi+E .

Однако основным недостатком полученных МНК-оценок неизвестных коэффициентов моделей регрессии, сводимых к линейному виду, является их смещённость.

Функцией потерь или ошибокназывается функционал вида

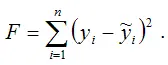
Также в качестве функции потерь может быть использована сумма модулей отклонений наблюдаемых значений результативного признака у от теоретических значений ỹ :

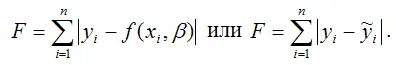
Функция потерь характеризует потери в точности аппроксимации исходных данных построенной моделью регрессии.

В интересах исследователя минимизировать функцию ошибок. Для этого используются различные методы, однако, их общий недостаток заключается в наличии локальных минимумов. Например, если оценка неизвестного параметра модели регрессии будет немного изменена, то значение функция потерь практически не изменится, но существует вероятность того, что ошибочное значение оцениваемого параметра модели регрессии даст в результате ощутимое уменьшение функции ошибок. Такое явление называется локальным минимумом.

Следствием локальных минимумов являются неоправданно завышенные или заниженные оценки неизвестных параметров модели регрессии.

Избежать попадания в локальный минимум можно путём повторения процедуры оценивания неизвестных параметров модели регрессии с изменёнными начальными условиями (шагом, ограничением оцениваемых параметров и т. д.).

При достижении функцией ошибок глобального минимума, оценки неизвестных коэффициентов модели регрессии считаются оптимальными.

К основным методам минимизации функции ошибок относятся:

1) метод Ньютона. В соответствии с данным методом основной шаг в направлении глобального минимума метода Ньютона рассчитывается по формуле:

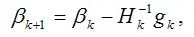
где βk – вектор значений оцениваемых параметров на k -ой итерации;

Н – матрица вторых частных производных, или матрица Гессе;

gk – вектор градиента на k -ой итерации.

Предположим, что задана скалярная функция у от переменных

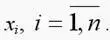
вида y=f(x).

Независимые переменные xi можно записать в виде вектора: x=[x1x2…xn]T. Тогда по определению производной:

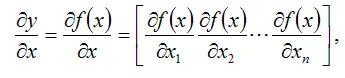
Вектор-столбец

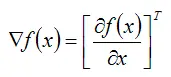
называется градиентом функции y=f(x) в точке x ;

2) для избежания громоздких вычислений матрицы Гессе существуют различные способы её замены приближёнными выражениями. Эти приёмы легли в основу квазиньютоновых методов. Суть квазиньютоновых методов заключается в том, что в различных точках вычисляются значения функции ошибок для определения первой и второй производной. Первая производная функции в заданной точке равна тангенсу угла наклона графика функции, а вторая производная функции в заданной точке равна скорости его изменения. Затем эти данные применяются для определения направления изменения параметров, а соответственно, и для минимизации функции ошибок;

3) симплекс-метод – это метод нелинейного оценивания, который не использует производные функции ошибок. При каждой итерации функция ошибок оценивается в n+1 точках n -мерного пространства, образуя при этом фигуру, называемую симплексом. В многомерном пространстве симплекс будет постепенно менять параметры, смещаясь в сторону минимизации функции потерь. Основное преимущество симплекс-метода перед остальными методами нелинейного оценивания заключается в том, что при слишком большом шаге для точного определения направления минимизации функции потерь или при слишком большом симплексе, алгоритм автоматически уменьшает симплекс, и вычислительная процедура продолжается. При обнаружении минимума, симплекс вновь увеличивается для проверки минимума на локальность.