Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

Но не всегда данная зависимость носит линейный характер. Если основные фонды, которые используются при производстве данной промышленной продукции, являются изношенным, то с увеличением показателя объема промышленного производства показатель себестоимости единицы произведённой промышленной продукции может также увеличиваться.

При условии, что изношенные основные фонды применяются для производства промышленной продукции до того момента, когда объём промышленного производства достигнет заранее определённого значения, можно построить кусочно-линейную модель регрессии. Предположим, что объём промышленного производства равен 500 единицам продукции. Тогда модель примет вид:

y=β0+β1x(x≤500)+β2x(x>500),

где y – себестоимость единицы промышленной продукции;

x – объём промышленного производства за месяц;

(x≤500 ) и ( x›500 ) – логические выражения, принимающие значения 1, если они истинны, или 0, если они ложны.

Данная кусочно-линейная модель регрессии зависит от общего свободного члена β0 и углового коэффициента. Угловой коэффициент может быть равен либо β1 (если выражение (x≤500 ) истинно, т. е. равно единице), либо β2 (если выражение ( x›500 ) истинно, т. е. равно единице).

Значение показателя объёма промышленной продукции, равное 500 единицам, считается точкой разрыва кривой регрессии.

Если же точка разрыва кривой регрессии не задана или её невозможно точно определить, то значение данной точки можно оценить с помощью дополнительного коэффициента, включённого в модель регрессии.

Заменим логические выражения в построенной кусочно-линейной модели регрессии на коэффициент β3 . В результате модель примет вид:

y=β0+β1x(x≤β3)+β2x(x>β3).

Собственно модели регрессии с точками разрыва характеризуются скачкообразными изменениями зависимой переменной в нескольких точках кривой регрессии. Кусочно-линейную модель регрессии можно преобразовать в собственно модель регрессии с точками разрыва.

Допустим, что при достижении основными фондами определённого уровня изношенности, себестоимость единицы промышленной продукции резко выросла, а затем продолжила медленно снижаться при условии увеличения объёмов производства данной продукции. В этом случае регрессионная зависимость примет вид:

y=(β0+β1x)(x≤500)+(β3+β2x)(x>500).

В связи с тем, что модели регрессии с точками разрыва являются внутренне нелинейными, то неизвестные параметры данных моделей нельзя оценить с помощью классического метода наименьших квадратов. Для оценки этих параметров применяются итерационные методы нелинейного оценивания и метод максимального правдоподобия.

Если в начале эконометрического моделирования перед исследователем стоит выбор между моделью регрессии, внутренне нелинейной и линейной моделью регрессии (или сводящейся к линейному виду), то предпочтение отдаётся линейным формам моделей.

Если модель регрессии является нелинейной по факторным переменным или нелинейной по оцениваемым коэффициентам, но внутренне линейной, то неизвестные коэффициенты данных моделей можно оценить с помощью классического метода наименьших квадратов.

Рассмотрим применение метода наименьших квадратов для определения неизвестных параметров модели регрессии, нелинейной по факторным переменным.

Параболическая функция второго порядка вида

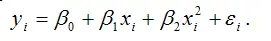
является моделью регрессии, нелинейной по факторным переменным xi .

Метод наименьших квадратов позволяет получить такие оценки параметров β0,β1 и β2 при которых сумма квадратов отклонений фактических значений результативного признака ỹ от расчетных (теоретических) β минимальна:

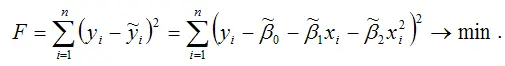
В процессе минимизации исходной функции регрессии неизвестными являются только значения коэффициентов β0,β1 и β2 , потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции трёх переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений.

Составим стационарную систему уравнений для функционала F , не пользуясь методом замен:

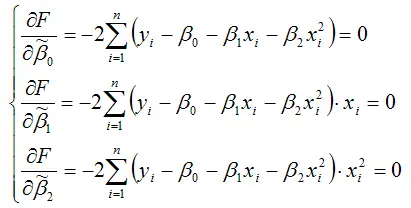
После элементарных преобразований стационарной системы уравнений, получим систему нормальных уравнений, позволяющую определить значения неизвестных коэффициентов параболической функции:

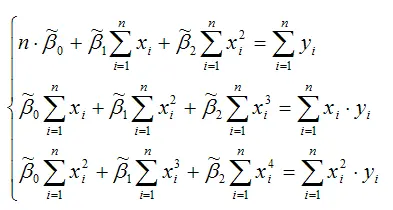
Данная система является системой нормальных уравнений относительно параметров

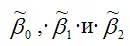
для параболической функции второго порядка.

Полученная система нормальных уравнений является квадратной, т. к. количество уравнений равняется количеству неизвестных переменных, поэтому коэффициенты

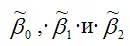
можно рассчитать с помощью метода Крамера или метода Гаусса .

Если рассматривать полиномиальную функцию n -ой степени вида

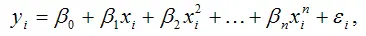
то для определения оценок неизвестных коэффициентов данной модели регрессии методом наименьших квадратов минимизируется функционал F :

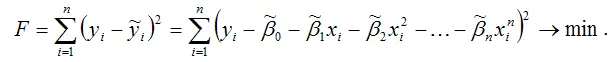
Для определения минимума функции нескольких переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений:

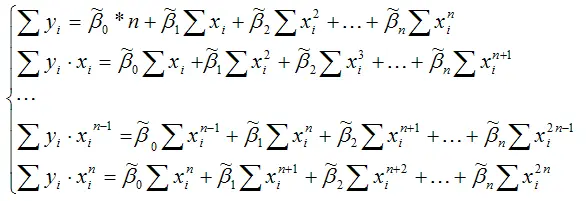
Решением данной стационарной системы уравнений будут оценки неизвестных коэффициентов полиномиальной функции n-ой степени.